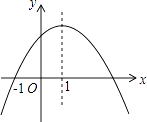题目内容
【题目】如图，抛物线y=﹣ 
x2+bx+c经过A（﹣1，0），B（0，2）两点，将△OAB绕点B逆时针旋转90°后得到△O′A′B′，点A落到点A′的位置．
（1）求抛物线对应的函数关系式；
（2）将抛物线沿y轴平移后经过点A′，求平移后所得抛物线对应的函数关系式；
（3）设（2）中平移后所得抛物线与y轴的交点为C，若点P在平移后的抛物线上，且满足△OCP的面积是△O′A′P面积的2倍，求点P的坐标；
（4）设（2）中平移后所得抛物线与y轴的交点为C，与x轴的交点为D，点M在x轴上，点N在平移后所得抛物线上，直接写出以点C，D，M，N为顶点的四边形是以CD为边的平行四边形时点N的坐标．
【答案】
（1）
解：如图1，把A（﹣1，0），B（0，2）两点坐标代入y=﹣ 
x2+bx+c得：
，
解得： 
，
∴抛物线对应的函数关系式：y=﹣ x2+ 
x+2
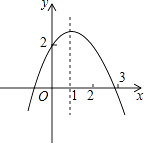
（2）
解：如图2，∵A（﹣1，0），B（0，2），
∴OA=1，OB=2，
由旋转得：O′B=OB=2，O′A′=OA=1，且旋转角∠OBO′=90°，
∴O′（2，2），A′（2，1），
所以由原抛物线从O′平移到A′可知，抛物线向下平移1个单位，
∴平移后所得抛物线对应的函数关系式：y=﹣ x2+ x+1
（3）
解：设P（a，﹣ a2+ a+1），
y=﹣ x2+ x+1，
当x=0时，y=1，
∴OC=A′O′=1，
根据点A（2，2）可分三种情况：
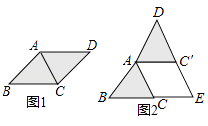
①当a＞2时，如图3，
∵S△OCP=2S△O′A′P，
∴ 
×1×a=2× ×1×（a﹣2），
a=4，
则y=﹣ a2+ a+1=﹣ ×42+ ×4+1=﹣ 
，
∴P（4，﹣ ），
②当0＜a＜2时，如图4，
∵S△OCP=2S△O′A′P，
∴ ×1×a=2× ×1×（2﹣a），
a= ，
则y=﹣ a2+ a+1=﹣ × 
2+ × +1= 
，
∴P（ ， ），
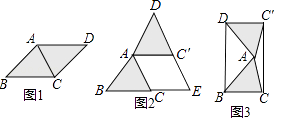
③当a＜0时，如图5，
同理得： ×1×（﹣a）=2× ×（﹣a+2），
a=4（不符合题意，舍），
综上所述，点P的坐标为（4，﹣ ）或（ ， ）
（4）
解：设N（m，﹣ m2+ m+1），
如图6，过N作NE⊥x轴于E，
∵四边形CMND是平行四边形，
∴CD∥MN，CD=MN，
∴∠CDO=∠MEN，
∵∠COD=∠MEN=90°，
∴△COD≌△NEM，
∴EN=CO，
∴ m2﹣ m﹣1=1，
解得：m=3或﹣1，
当m=3时，y=﹣1，
当m=﹣1时，y=﹣1，
∴N（3，﹣1）或（﹣1，﹣1），
如图7就是点N（﹣1，﹣1）时，所成的平行四边形；
如图8和如图9，
∵四边形CDMN是平行四边形，
∴CN∥DM，
∴点C与点N是对称点，
∵C（0，1），对称轴是x=﹣ 
=1，
∴N（2，1），
综上所述，点N的坐标为（3，﹣1）或（﹣1，﹣1）或（2，1）．
【解析】（1）如图1，利用待定系数法求二次函数的关系式；（2）如图2，根据旋转得出点O′（2，2），A′（2，1），知道原抛物线从向下平移1个单位得到新抛物线，根据原抛物线的关系式可以写出新抛物线的函数关系式；（3）设P（a，﹣ a2+ a+1），根据点P的位置和A′的横坐标2可以分为三种情况：①当a＞2时，如图3，②当0＜a＜2时，如图4，③当a＜0时，如图5，分别根据S△OCP=2S△O′A′P ， 列等式求出a的值，并求出对应P的坐标；（4）如图6，因为点N在平移后所得抛物线上，所以设N（m，﹣ m2+ m+1），作辅助线，构建全等三角形，发现点N的纵坐标的绝对值为1，由此列式为： m2﹣ m﹣1=1，解出m的值，求出点N的坐标．同理如图7得出点N的坐标．
如图8和9，点C与点N是对称点，根据点C的坐标求点N的坐标．
【考点精析】认真审题，首先需要了解二次函数的图象(二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点)，还要掌握二次函数的性质(增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小)的相关知识才是答题的关键．
