题目内容
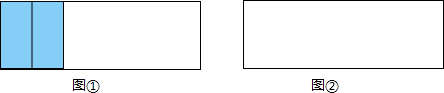
在1×3的矩形内不重叠地放两个与大矩形相似的小矩形,且每个小矩形的每条边相应地与大矩形的一条边平行,求两个小矩形周长和的最大值.分析:由于小矩形放置的位置不确定,故应分三种情况讨论:
(1)两个小矩形都“竖放”;(2)两个小矩形都“横放”;(3)两个小矩形一个“横放”,一个“竖放”.
(1)两个小矩形都“竖放”;(2)两个小矩形都“横放”;(3)两个小矩形一个“横放”,一个“竖放”.
解答: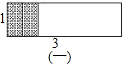 解:两个小矩形的放置情况有如下几种:
解:两个小矩形的放置情况有如下几种:
(1)两个小矩形都“竖放”,如图(一),在这种放法下,周长和最大的两个小矩形,边长分别为1和
,
故此时周长和的最大值为
.
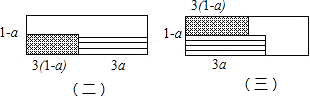
(2)两个小矩形都“横放”,如图(二)及图(三)所示,这时两个小矩形的周长和的最大值是
2(a+3a)+2[1-a+3(1-a)]=8.
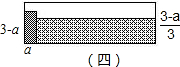
(3)两个小矩形一个“横放”,一个“竖放”,如图(四),这时两个小矩形的周长和为
2(a+3a)+2(3-a+
)=8+
,
因为0<3a≤1,即0<a≤
,故当a=
时,此时两个小矩形的周长和最大为
,
综上三种情形,知所求的最大值为
.
故答案为:
.
 解:两个小矩形的放置情况有如下几种:
解:两个小矩形的放置情况有如下几种:(1)两个小矩形都“竖放”,如图(一),在这种放法下,周长和最大的两个小矩形,边长分别为1和
| 1 |
| 3 |
故此时周长和的最大值为
| 16 |
| 3 |
(2)两个小矩形都“横放”,如图(二)及图(三)所示,这时两个小矩形的周长和的最大值是
2(a+3a)+2[1-a+3(1-a)]=8.

(3)两个小矩形一个“横放”,一个“竖放”,如图(四),这时两个小矩形的周长和为
2(a+3a)+2(3-a+
| 3-a |
| 3 |
| 16a |
| 3 |
因为0<3a≤1,即0<a≤
| 1 |
| 3 |
| 1 |
| 3 |
| 88 |
| 9 |

综上三种情形,知所求的最大值为
| 88 |
| 9 |
故答案为:
| 88 |
| 9 |
点评:本题考查的是相似多边形的对应边成比例,利用分类讨论的思想进行分析是解答此题的关键.

练习册系列答案
相关题目