题目内容
 (1)如图,已知
(1)如图,已知 ,求
,求 的值;
的值;
(2)如果 ,那么
,那么 成立吗?为什么?
成立吗?为什么?
解:(1)∵由
得:a=3b,c=3d,
∴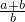 =
= =
= =4;
=4;
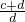 =
= =4;
=4;
(2) 成立.
成立.
理由:∵设 ,
,
则:a=kb,c=kd,
∴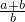 =
= =
= =k+1,
=k+1,
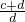 =
= =k+1,
=k+1,
∴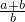 =
=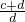 成立.
成立.
分析:(1)由 得出a=3b,c=3d,代入求出即可;
得出a=3b,c=3d,代入求出即可;
(2)设 ,得出a=kb,c=kd,代入求出
,得出a=kb,c=kd,代入求出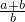 和
和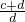 的值,根据结果即可得出答案.
的值,根据结果即可得出答案.
点评:本题考查了平行线分线段成比例定理和比例的性质,主要考查学生灵活运用比例的性质进行计算的能力.

得:a=3b,c=3d,
∴
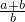 =
= =
= =4;
=4;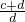 =
= =4;
=4;(2)
 成立.
成立.理由:∵设
 ,
,则:a=kb,c=kd,
∴
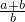 =
= =
= =k+1,
=k+1,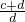 =
= =k+1,
=k+1,∴
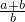 =
=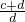 成立.
成立.分析:(1)由
 得出a=3b,c=3d,代入求出即可;
得出a=3b,c=3d,代入求出即可;(2)设
 ,得出a=kb,c=kd,代入求出
,得出a=kb,c=kd,代入求出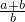 和
和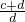 的值,根据结果即可得出答案.
的值,根据结果即可得出答案.点评:本题考查了平行线分线段成比例定理和比例的性质,主要考查学生灵活运用比例的性质进行计算的能力.

练习册系列答案
相关题目



 ,
,

 的度数
的度数 ,求
,求 的值;
的值; ,那么
,那么 成立吗?为什么?
成立吗?为什么?
 ,求作一点
,求作一点 ,使
,使 的两边的距离相等,且
的两边的距离相等,且 .下列确定
.下列确定
 、
、 两角平分线的交点;
两角平分线的交点; 、
、 的垂直平分线的交点;
的垂直平分线的交点; 、
、 、
、 、
、