题目内容
已知二次函数y=x2+bx+3的图象经过点（3，0）．
（1）求b的值；
（2）求出该二次函数图象的顶点坐标；
（3）在所给坐标系中画出该函数的图象（不要求列对应数值表，但要求尽可能画准确）．
解：（1）∵二次函数y=x2+bx+3的图象经过点（3，0）．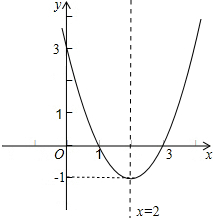
∴9+3b+3=0，
∴b=-4；
（2）∵y=x2-4x+3=（x-2）2-1
∴该二次函数图象的顶点坐标为（2，-1）；
（3）描点作图如下：
分析：（1）把（3，0）代入y=x2+bx+3可解得b的值；
（2）把y=x2-4x+3进行配方得到y=（x-2）2-1，然后根据顶点式写出顶点坐标；
（3）抛物线的对称轴为直线x=2，顶点坐标为（2，-1），与y轴的交点坐标为（0，3），与x轴的交点坐标为（1，0）、（3，0），然后根据这些特征进行画图．
点评：本题考查了二次函数的图象：二次函数y=ax2+bx+c（a≠0）的图象为抛物线，当a＞0；抛物线的顶点式为y=a（x-
）2+
，它的对称轴为直线x=-，顶点坐标为（-，；抛物线与y轴的交点坐标为（0，c）．
∴9+3b+3=0，
∴b=-4；
（2）∵y=x2-4x+3=（x-2）2-1
∴该二次函数图象的顶点坐标为（2，-1）；
（3）描点作图如下：
分析：（1）把（3，0）代入y=x2+bx+3可解得b的值；
（2）把y=x2-4x+3进行配方得到y=（x-2）2-1，然后根据顶点式写出顶点坐标；
（3）抛物线的对称轴为直线x=2，顶点坐标为（2，-1），与y轴的交点坐标为（0，3），与x轴的交点坐标为（1，0）、（3，0），然后根据这些特征进行画图．
点评：本题考查了二次函数的图象：二次函数y=ax2+bx+c（a≠0）的图象为抛物线，当a＞0；抛物线的顶点式为y=a（x-
）2+，它的对称轴为直线x=-，顶点坐标为（-，；抛物线与y轴的交点坐标为（0，c）． 
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
已知二次函数y=x2+（2a+1）x+a2-1的最小值为0，则a的值是（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知二次函数y=-x2+2x+m的部分图象如图所示，则关于x的一元二次方程-x2+2x+m=0的解为（ ）| A、x1=1，x2=3 | B、x1=0，x2=3 | C、x1=-1，x2=1 | D、x1=-1，x2=3 |
已知二次函数y=-x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（-1，0），与y轴的交点坐标为（0，3）．