题目内容
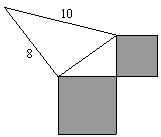
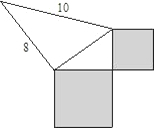如图，两阴影部分都是正方形，如果两正方形面积之比为1：2，那么，两正方形的面积分别为________．
12，24
分析：首先根据已知直角三角形的两边运用勾股定理求得斜边是6．再根据勾股定理以及正方形的面积公式，知：两个正方形的面积和等于36，又两正方形面积之比为1：2，则两个正方形的面积分别是12，24．
解答：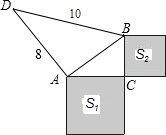
解：如图所示，
在Rt△ABD中，∵BD=10，AD=8，∴AB2=BD2-AD2=36．
即在Rt△ABC中，AC2+BC2=AB2=36，
∴S1+S2=36
又S2：S1=1：2
解之得：S1=24，S2=12．
故答案为，12，24．
点评：本题考查了勾股定理以及正方形的面积公式．
分析：首先根据已知直角三角形的两边运用勾股定理求得斜边是6．再根据勾股定理以及正方形的面积公式，知：两个正方形的面积和等于36，又两正方形面积之比为1：2，则两个正方形的面积分别是12，24．
解答：
解：如图所示，在Rt△ABD中，∵BD=10，AD=8，∴AB2=BD2-AD2=36．
即在Rt△ABC中，AC2+BC2=AB2=36，
∴S1+S2=36
又S2：S1=1：2
解之得：S1=24，S2=12．
故答案为，12，24．
点评：本题考查了勾股定理以及正方形的面积公式．
练习册系列答案
一课一练课时达标系列答案
相关题目
13、如图，两阴影部分都是正方形，如果两正方形面积之比为1：2，那么，两正方形的面积分别为
