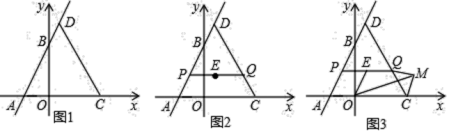Question

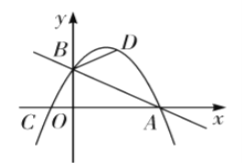
【题目】综合与探究 如图，在平面直角坐标系中，直线与轴交于点，与轴交于点，抛物线经过两点且与轴的负半轴交于点．

（1）求该抛物线的解析式；

（2）若为直线上方抛物线上的一个动点，当时，求点的坐 标；

（3）已知分别是直线和抛物线上的动点，当以为顶点的四边形 是平行四边形，且以为边时，请直接写出所有符合条件的点的坐标．

Answer 1

【答案】（1）；（2）点的坐标为；（3）点的坐标为或或．

【解析】

（1）求得A，B两点的坐标，代入抛物线的解析式，获得b，c的值，即可求出抛物线的解析式；

（2）通过平行线分割2倍角条件，得到相等的角关系，利用等角的三角函数值相等，得到点的坐标；

（3）B，O，E，F四点作平行四边形，当OB为边时，以EF=OB的关系建立方程求解.

解：在中，令得，令得

把代入，

得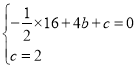

解得：

抛物线的解析式为

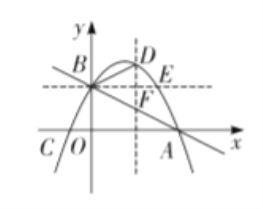
如图，过点作轴的平行线交抛物线于点，过点作的垂线，垂足为点

轴

即

设点的坐标为

则

，

即

解得：

经检验，是分式方程的解

当时，

点的坐标为

点的坐标为或

当BO为边时，OB∥EF，OB=EF

设E(m,m+2)，F(m, m2+m+2)

EF==2

解得=2，，

当=2时，m+2=×2+2=1；

当时，m+2=×（2-2）+2=1+；

当时，m+2=×（2+2）+2=1-

∴E点的坐标为(2,1)或(2-2,1+)或(2+2,1-).

故答案为（1）；（2）点的坐标为；（3）点的坐标为或或．