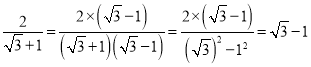题目内容
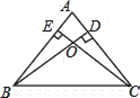
【题目】如图,四边形![]() 是菱形,
是菱形,![]() 在
在![]() 上,
上,![]() 在
在![]() 延长线上,
延长线上,![]() 和
和![]() 相交于点
相交于点![]() ,若
,若![]() ,
,![]() ,
,![]() 的长为
的长为![]() ,则菱形
,则菱形![]() 的面积为________.
的面积为________.

【答案】![]()
【解析】
连接AC、BD,交于点O,分别取AE、BF的中点M、N,连接OM、ON,在AB上截取AH=AM,连接OH,过C作CP⊥AF于P,根据中位线定理可得到OM=![]() CE,ON=
CE,ON=![]() DF,则有OM=ON,证明△AMO≌△AHO,得OM=OH=ON,继而可得∠AMO+∠ONH=180,再根据平行线的性质可得∠DAB+∠EGF=180°,从而得∠DAB=30°,继而根据含30度角的直角三角形的性质求出菱形高PC的长,代入面积公式即可求得答案.
DF,则有OM=ON,证明△AMO≌△AHO,得OM=OH=ON,继而可得∠AMO+∠ONH=180,再根据平行线的性质可得∠DAB+∠EGF=180°,从而得∠DAB=30°,继而根据含30度角的直角三角形的性质求出菱形高PC的长,代入面积公式即可求得答案.
连接AC、BD,交于点O,分别取AE、BF的中点M、N,连接OM、ON,在AB上截取AH=AM,连接OH,过C作CP⊥AF于P,
∵四边形ABCD是菱形,
∴O是BD的中点,也是AC的中点,
∴OM=![]() CE,ON=
CE,ON=![]() DF,
DF,
∵CE=DF,
∴OM=ON,
∵AC平分∠DAB,
∴∠DAC=∠BAC,
∵AO=AO,
∴△AMO≌△AHO,
∴OM=OH,∠AMO=∠AHO,
∴OM=OH=ON,
∴∠OHN=∠ONH,
∵∠AHO+∠OHN=180°,
∴∠AMO+∠ONH=180,
∵OM∥EC,ON∥DF,
∴∠AMO=∠AEC,∠ONH=∠GFA,
∴∠AEC+∠GFA=180°,
∴∠DAB+∠EGF=180°,
∵∠CGF=30°,
∴∠EGF=150°,
∴∠DAB=30°,
∵AD∥BC,
∴∠CBF=∠DAB=30°,
∵AB=BC=6,
∴CP=![]() BC=3,
BC=3,
∴菱形ABCD的面积=ABCP=6×3=18,
故答案为:18.

【题目】如图,在△ABC中,AB=4.41cm,BC=8.83cm,P是BC上一动点,连接AP,设P,C两点间的距离为xcm,P,A两点间的距离为ycm.(当点P与点C重合时,x的值为0)小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如表:
x/cm | 0 | 0.43 | 1.00 | 1.50 | 1.85 | 2.50 | 3.60 | 4.00 | 4.30 | 5.00 | 5.50 | 6.00 | 6.62 | 7.50 | 8.00 | 8.83 |
y/cm | 7.65 | 7.28 | 6.80 | 6.39 | 6.11 | 5.62 | 4.87 |
| 4.47 | 4.15 | 3.99 | 3.87 | 3.82 | 3.92 | 4.06 | 4.41 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当PA=PC时,PC的长度约为 cm.(结果保留一位小数)