题目内容
如图，在直角坐标系中，P是第一象限内的点，其坐标是（3，m），且OP与x轴正半轴的夹角α的正切值是
，则sinα的值为
- A.
- B.
- C.
- D.
A
分析：过点P作PE⊥x轴于点E，则可得OE=3，PE=m，在Rt△POE中求出OP，继而可得sinα的值．
解答：过点P作PE⊥x轴于点E，
则可得OE=3，PE=m，
在Rt△POE中，tanα=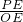
=，
解得：m=4，
则OP=
=5，
故sinα=．
故选A．
点评：本题考查了勾股定理及同角的三角函数关系，解答本题的关键是求出OP的长度．
分析：过点P作PE⊥x轴于点E，则可得OE=3，PE=m，在Rt△POE中求出OP，继而可得sinα的值．
解答：过点P作PE⊥x轴于点E，
则可得OE=3，PE=m，
在Rt△POE中，tanα=
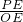=，解得：m=4，
则OP=
=5，故sinα=
．故选A．
点评：本题考查了勾股定理及同角的三角函数关系，解答本题的关键是求出OP的长度．
练习册系列答案
相关题目
如图，在直角坐标系中，点P的坐标为（3，4），将OP绕原点O逆时针旋转90°得到线段OP′．
，2）．画出△ABC的两个位似图形△A1B1C1，△A2B2C2，同时满足下列两个条件：