题目内容
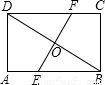
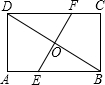 如图所示,有两条笔直的公路BD和EF(宽度不计),从一块矩形的土地ABCD中穿过,已知EF是BD的垂直平分线,BD=40米,EF=30 米,求四边形BEDF的面积.
如图所示,有两条笔直的公路BD和EF(宽度不计),从一块矩形的土地ABCD中穿过,已知EF是BD的垂直平分线,BD=40米,EF=30 米,求四边形BEDF的面积.
分析:连接DE、BF,因为四边形ABCD是矩形,所以AB∥CD,进而求证DF=BE,再求证FD=FB,即可判定四边形BFDE是菱形,根据菱形面积计算公式即可计算菱形BFDE的面积.
解答: 解:如图,连接DE、BF,
解:如图,连接DE、BF,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠ODF=∠OBE,
由EF垂直平分BD,
得OD=OB,∠DOF=∠BOE=90°,
∴△DOF是△BOE成旋转对称,
故DF=BE,
∴四边形BEDF是平行四边形,
又∵EF是BD的垂直平分线,
∴FD=FB,
因此BFDE是菱形,
∴S菱形BFDE=
EF•BD=
×30×40=600(米2).
 解:如图,连接DE、BF,
解:如图,连接DE、BF,∵四边形ABCD是矩形,
∴AB∥CD,
∴∠ODF=∠OBE,
由EF垂直平分BD,
得OD=OB,∠DOF=∠BOE=90°,
∴△DOF是△BOE成旋转对称,
故DF=BE,
∴四边形BEDF是平行四边形,
又∵EF是BD的垂直平分线,
∴FD=FB,
因此BFDE是菱形,
∴S菱形BFDE=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了菱形的判定,矩形对边相等且平行的性质,垂直平分线的性质,本题中求证DF=BE是解题的关键.

练习册系列答案
相关题目


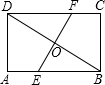 如图所示,有两条笔直的公路BD和EF(宽度不计),从一块矩形的土地ABCD中穿过,已知EF是BD的垂直平分线,BD=40米,EF=30 米,求四边形BEDF的面积.
如图所示,有两条笔直的公路BD和EF(宽度不计),从一块矩形的土地ABCD中穿过,已知EF是BD的垂直平分线,BD=40米,EF=30 米,求四边形BEDF的面积.