题目内容
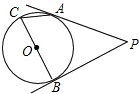 如图,从点P向⊙O引两条切线PA,PB,A、B为切点,AC为弦,BC是直径.若∠P=60°,PB=2cm,求AC.
如图,从点P向⊙O引两条切线PA,PB,A、B为切点,AC为弦,BC是直径.若∠P=60°,PB=2cm,求AC.
分析:根据PA,PB是切线,∠P=60°,判断出△ABP是正三角形,根据CB⊥BP,判断出∠CBP为90°,
进而得出∠ABC=30°,再利用三角函数求出AC的长.
进而得出∠ABC=30°,再利用三角函数求出AC的长.
解答: 解:如图所示:
解:如图所示:
连接AB,
∵PA,PB是切线,
∴PA=PB.(2分)
又∵∠P=60°,
∴AB=PB=2cm,(1分)
∵BC是直径,
∴∠BAC=90°.(2分)
又CB⊥PB,而∠PBA=60°,
∴∠ABC=30°.(1分)
则AC=ABtan30°=
(cm).
 解:如图所示:
解:如图所示:连接AB,
∵PA,PB是切线,
∴PA=PB.(2分)
又∵∠P=60°,
∴AB=PB=2cm,(1分)
∵BC是直径,
∴∠BAC=90°.(2分)
又CB⊥PB,而∠PBA=60°,
∴∠ABC=30°.(1分)
则AC=ABtan30°=
2
| ||
| 3 |
点评:此题要根据切线的性质、切线长定理和直径所对的圆周角是90°,找到图中的直角三角形,根据直角三角形的性质解题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 如图,从点P向⊙O引两条切线PA,PB,切点为A,B,BC为⊙O的直径,若∠P=60°,PA=3,则⊙O的直径BC的长为( )
如图,从点P向⊙O引两条切线PA,PB,切点为A,B,BC为⊙O的直径,若∠P=60°,PA=3,则⊙O的直径BC的长为( )A、2
| ||||
B、
| ||||
| C、3 | ||||
D、4
|
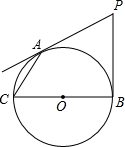 如图,从点P向⊙O引两条切线PA、PB,切点A、B,BC为⊙O的直径,若∠P=60°,PA=6,求AC的长.
如图,从点P向⊙O引两条切线PA、PB,切点A、B,BC为⊙O的直径,若∠P=60°,PA=6,求AC的长.