Question

【题目】如图，在中，，DE是过点A的直线，于点D，于点E，．

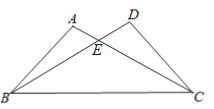
若BC在DE的同侧如图求证：．

若BC在DE的两侧如图，其他条件不变，中的结论还成立吗？不需证明

Answer 1

【答案】（1）详见解析；（2）AB⊥AC.

【解析】

（1）根据直角三角形全等的判定方法HL易证得△ABD≌△CAE，可得∠DAB=∠ACE，再根据三角形内角和定理即可证得结论；（2）与（1）同理结论仍成立．

（1）证明：∵BD⊥DE于点D，CE⊥DE于点E，

∴△ABD和△CAE均为直角三角形．

在Rt△ABD和Rt△CAE中，，

∴Rt△ABD≌Rt△CAE（HL），

∴∠ABD=∠CAE．

又∵∠ABD+∠BAD=90°，

∴∠CAE+∠BAD=90°，

∴∠BAC=180°﹣（∠CAE+∠BAD）=90°，

∴AB⊥AC．

（2）解：AB⊥AC，理由如下：

同（1）可证出：Rt△ABD≌Rt△CAE（HL），

∴∠ABD=∠CAE．

又∵∠ABD+∠BAD=90°，

∴∠BAC=∠CAE+∠BAD=90°，

∴AB⊥AC．