题目内容
 如图,P是∠ABC的边BC上一点,sin∠ABC=
如图,P是∠ABC的边BC上一点,sin∠ABC= ,BP=9,⊙P的半径为5.点O是射线BC上的一个动点,以O为圆心作圆,使⊙O与射线BA相切,同时又与⊙P相切,则⊙O的半径为________.
,BP=9,⊙P的半径为5.点O是射线BC上的一个动点,以O为圆心作圆,使⊙O与射线BA相切,同时又与⊙P相切,则⊙O的半径为________.
7,1, 和2
和2
分析:⊙P同时与⊙O和射线BA相切应分两种情况分类讨论:①当⊙P与⊙O外切;②当⊙P与⊙O内切.
解答:设⊙O的半径为r.设⊙O与射线BA相切于点D,连接OD,则∠BDO=90°.
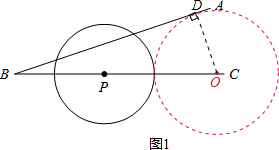
①如图1,∵sin∠ABC= ,BP=9,⊙P的半径为5,
,BP=9,⊙P的半径为5,
∴ =
=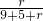 =
= ,
,
解得r=7;
②如图2,∵sin∠ABC= ,BP=9,⊙P的半径为5,
,BP=9,⊙P的半径为5,
∴ =
=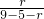 =
= ,
,
解得r=1;
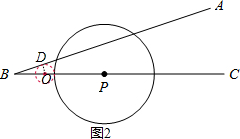
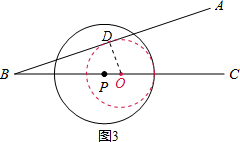
③如图3,∵sin∠ABC= ,BP=9,⊙P的半径为5,
,BP=9,⊙P的半径为5,
∴ =
=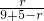 =
= ,
,
解得r= ;
;
④如图④,∵sin∠ABC= ,BP=9,⊙P的半径为5,
,BP=9,⊙P的半径为5,
∴ =
=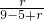 =
= ,
,
解得r=2;
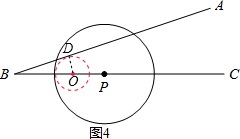
综合①②③④所述,符合条件的⊙O的半径是7,1, 和2.
和2.
故答案是:7,1, 和2.
和2.
点评:本题综合考查了直线与圆相切和两圆相切的知识,对学生建立系统的与圆相切有关的知识体系有很好的促进作用.
 和2
和2分析:⊙P同时与⊙O和射线BA相切应分两种情况分类讨论:①当⊙P与⊙O外切;②当⊙P与⊙O内切.
解答:设⊙O的半径为r.设⊙O与射线BA相切于点D,连接OD,则∠BDO=90°.
①如图1,∵sin∠ABC=
 ,BP=9,⊙P的半径为5,
,BP=9,⊙P的半径为5,∴
 =
=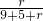 =
= ,
,解得r=7;

②如图2,∵sin∠ABC=
 ,BP=9,⊙P的半径为5,
,BP=9,⊙P的半径为5,∴
 =
=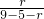 =
= ,
,解得r=1;

③如图3,∵sin∠ABC=
 ,BP=9,⊙P的半径为5,
,BP=9,⊙P的半径为5,∴
 =
=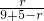 =
= ,
,解得r=
 ;
;
④如图④,∵sin∠ABC=
 ,BP=9,⊙P的半径为5,
,BP=9,⊙P的半径为5,∴
 =
=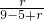 =
= ,
,解得r=2;

综合①②③④所述,符合条件的⊙O的半径是7,1,
 和2.
和2.故答案是:7,1,
 和2.
和2.点评:本题综合考查了直线与圆相切和两圆相切的知识,对学生建立系统的与圆相切有关的知识体系有很好的促进作用.

练习册系列答案
相关题目
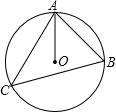 如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )
如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )| A、28° | B、30° | C、31° | D、62° |
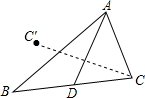 如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为
如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为 15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
 如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( )
如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( ) 如图,AD是△ABC的外接圆直径,AD=
如图,AD是△ABC的外接圆直径,AD=