题目内容
如图,经过点A(-2,0)的一次函数 y=ax+b(a≠0) 与反比例函数 y= (k≠0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB=
(k≠0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB= ,点B的坐标为(4,0).
,点B的坐标为(4,0).
(1) 求反比例函数和一次函数的解析式;
(2)设一次函数与y轴相交于点C,求四边形OBPC的面积.
解:(1)∵ A(-2,0),B(4,0),∴ AB=6.
∵ tan∠PAB= , ∴
, ∴  , 得BP=
, 得BP= . ∴ P(4,
. ∴ P(4, ) .
) .
把P(4, )代入y=
)代入y= 中,得 k=36.
中,得 k=36.
∴ 反比例函数的解析式为 y= .
.
将A(-2,0), P(4, ) 代入y=ax+b中,得
) 代入y=ax+b中,得 
解得 
∴ 一次函数的解析式为 y= .
.
(2)由(1)得C(0, ).
).
由题设可知四边形OBPC是直角梯形,
∴四边形OBPC的面积为S= (OC+BP)×OB=
(OC+BP)×OB= ×
× ×4=24.
×4=24.
解析

练习册系列答案
相关题目



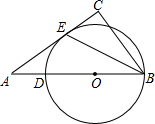 (2011•辽阳)如图,⊙O经过点B、D、E,BD是⊙O的直径,∠C=90°,BE平分∠ABC.
(2011•辽阳)如图,⊙O经过点B、D、E,BD是⊙O的直径,∠C=90°,BE平分∠ABC.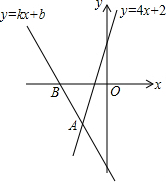 (2013•南通)如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为
(2013•南通)如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为 0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB=
0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB=