题目内容
 如图,BD是∠ABC的角平分线,DE⊥AB于点E,DF⊥BC于点F,S△ABC=36cm2,AB=18cm,BC=12cm,则DE的长为________cm.
如图,BD是∠ABC的角平分线,DE⊥AB于点E,DF⊥BC于点F,S△ABC=36cm2,AB=18cm,BC=12cm,则DE的长为________cm.

分析:把S△ABC=36cm2分成两部分即△ABD和△BCD,利用三角形的面积公式可得等量关系式,求这个等量关系即可.
解答:∵BD是∠ABC的角平分线,DE⊥AB,DF⊥BC,
∴DE=DF,
∵S△ABC=36cm2,S△BCD=
 BC•DF,
BC•DF,又∵S△ABC=S△ABD+S△BCD,AB=18cm,BC=12cm,
∴
 ×18•DE+
×18•DE+ ×12•DF=36,
×12•DF=36,∴9DE+6DF=36.
又∵DE=DF,
∴9DE+6DE=36,
∴DE=
 cm.
cm.点评:本题主要考查了三角形的面积公式和角的平分线上的点到角的两边的距离相等的性质.解题的关键是得到DE=DF.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数.
25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数. 如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=
如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=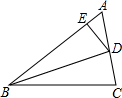 如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.
如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长. 如图,BD是△ABC的角平分线,且BD=BC=AD.
如图,BD是△ABC的角平分线,且BD=BC=AD. 如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是
如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是