题目内容
【题目】阅读材料:由绝对值的意义可知:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .利用这一特性,可以帮助我们解含有绝对值的方程.比如:方程
.利用这一特性,可以帮助我们解含有绝对值的方程.比如:方程![]() ,
,
当![]() 时,原方程可化为
时,原方程可化为![]() ,解得
,解得![]() ;
;
当![]() 时,原方程可化为
时,原方程可化为![]() ,解得
,解得![]() .
.
所以原方程的解是![]() 或
或![]() .
.
(1)请补全题目中横线上的结论.
(2)仿照上面的例题,解方程:![]() .
.
(3)若方程![]() 有解,则
有解,则![]() 应满足的条件是 .
应满足的条件是 .
【答案】(1)a,-a;(2)x=![]() 或x=
或x=![]() ,见解析;(3)m≥1
,见解析;(3)m≥1
【解析】
(1)根据绝对值化简填空即可;(2)根据绝对值的性质分3x+1≥0和3x+1≤0两种情况讨论;(3)根据绝对值非负性列出不等式解答即可.
解:(1)a,-a
(2)原方程化为![]()
当3x+1≥0时,方程可化为3x+1=5,解得:x=![]()
当3x+1≤0时,方程可化为3x+1=-5,解得:x=![]()
所以原方程的解是x=![]() 或x=
或x=![]()
(3)∵方程![]() 有解
有解
∴![]()
m≥1

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
【题目】甲、乙两名队员参加射击训练,成绩分别绘制成下列两个统计图:
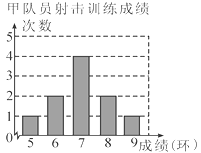
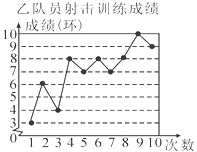
根据以上信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?