题目内容
设（a-b-2）2+|c+2d|=-|3c+d-5|-（a-2b+1）2，则（a+b+c+d）（a+b+c-d）（a-b+c+d）（a-b-c-d）=
- A.0
- B.297
- C.-297
- D.495
B
分析：根据非负数的性质得到关于a、b的二元一次方程组，关于c、d的二元一次方程组，然后分别解方程组求出a、b、c、d的值，再代入代数式进行计算即可求解．
解答：∵（a-b-2）2+|c+2d|=-|3c+d-5|-（a-2b+1）2，
∴（a-b-2）2+|c+2d|+|3c+d-5|+（a-2b+1）2=0，
∴
，
，
解得
，
，
∴（a+b+c+d）（a+b+c-d）（a-b+c+d）（a-b-c-d），
=（5+3+2-1）（5+3+2+1）（5-3+2-1）（5-3-2+1），
=9×11×3×1，
=297．
故选B．
点评：本题考查了绝对值非负数，平方数非负数的性质，根据几个非负数的和等于0，则每一个算式都等于0列式是解题的关键，本题运算量比较大，计算时要仔细．
分析：根据非负数的性质得到关于a、b的二元一次方程组，关于c、d的二元一次方程组，然后分别解方程组求出a、b、c、d的值，再代入代数式进行计算即可求解．
解答：∵（a-b-2）2+|c+2d|=-|3c+d-5|-（a-2b+1）2，
∴（a-b-2）2+|c+2d|+|3c+d-5|+（a-2b+1）2=0，
∴
，，解得
，，∴（a+b+c+d）（a+b+c-d）（a-b+c+d）（a-b-c-d），
=（5+3+2-1）（5+3+2+1）（5-3+2-1）（5-3-2+1），
=9×11×3×1，
=297．
故选B．
点评：本题考查了绝对值非负数，平方数非负数的性质，根据几个非负数的和等于0，则每一个算式都等于0列式是解题的关键，本题运算量比较大，计算时要仔细．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
八年级某班级部分同学去植树，若每人平均植树7棵，还剩9棵，若每人平均植树9棵，则有1名同学植树的棵数不到8棵．若设同学人数为x人，下列各项能准确的求出同学人数与种植的树木的数量的是（ ）
| A、7x+9-9（x-1）＞0 | |||||
| B、7x+9-9（x-1）＜8 | |||||
C、
| |||||
D、
|
已知⊙O1的半径为R，周长为C．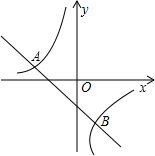
如图，若反比例函数y=-