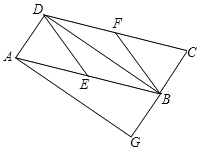
题目内容
【题目】如图,△ABC和△ADE中,![]() ,
,![]() ,边AD与边BC交于点P(不与点B,C重合),点B,E在AD异侧,AI、CI分别平分
,边AD与边BC交于点P(不与点B,C重合),点B,E在AD异侧,AI、CI分别平分![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)设![]() ,请用含
,请用含![]() 的式子表示PD,并求PD的最大值;
的式子表示PD,并求PD的最大值;
(3)当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ,分别直接写出m,n的值.
,分别直接写出m,n的值.
【答案】(1)见详解;(2)6-x,3; (3) ![]()
【解析】
(1)由条件易证△ABC≌△ADE,得∠BAC=∠DAE,即可得出结论.
(2)PD=AD﹣AP=6﹣x.AP的最小值即AP⊥BC时AP的长度,此时PD可得最大值.
(3)应用三角形内角定理及角平分线定义即可表示出∠AIC,从而得到m,n的值.
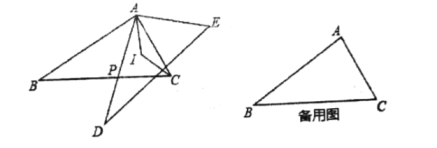
(1)在△ABC和△ADE中,(如图1)
∵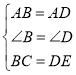 ,∴△ABC≌△ADE(SAS),∴∠BAC=∠DAE,
,∴△ABC≌△ADE(SAS),∴∠BAC=∠DAE,
即∠BAD+∠DAC=∠DAC+∠CAE,∴∠BAD=∠CAE.
(2)∵AD=6,AP=x,∴PD=6﹣x.
当AD⊥BC时,AP![]() AB=3最小,即PD=6﹣3=3为PD的最大值.
AB=3最小,即PD=6﹣3=3为PD的最大值.
(3)如图2,设∠BAP=α,则∠APC=α+30°.
∵AB⊥AC,∴∠BAC=90°,∠PCA=60°,∠PAC=90°﹣α.
∵AI、CI分别平分∠PAC,∠PCA,
∴∠IAC![]() ∠PAC,∠ICA
∠PAC,∠ICA![]() ∠PCA,
∠PCA,
∴∠AIC=180°﹣(∠IAC+∠ICA)=180°![]() (∠PAC+∠PCA)=180°
(∠PAC+∠PCA)=180°![]() (90°﹣α+60°)
(90°﹣α+60°)
![]() α+105°.
α+105°.
∵0<α<90°,∴105°![]() α+105°<150°,即105°<∠AIC<150°,∴m=105,n=150.
α+105°<150°,即105°<∠AIC<150°,∴m=105,n=150.


练习册系列答案
相关题目