题目内容
如图,在直角坐标系xOy中,直线 与双曲线
与双曲线 相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
(1)求m、n的值;
(2)求直线AC的解析式.
(1)m=-1,n=-1;(2)y=- x+
x+
解析试题分析:(1)由直线 与双曲线
与双曲线 相交于A(-1,a)、B两点可得B点横坐标为1,点C的坐标为(1,0),再根据△AOC的面积为1可求得点A的坐标,从而求得结果;
相交于A(-1,a)、B两点可得B点横坐标为1,点C的坐标为(1,0),再根据△AOC的面积为1可求得点A的坐标,从而求得结果;
(2)设直线AC的解析式为y=kx+b,由图象过点A(-1,1)、C(1,0)根据待定系数法即可求的结果.
(1)∵直线 与双曲线
与双曲线 相交于A(-1,a)、B两点,
相交于A(-1,a)、B两点,
∴B点横坐标为1,即C(1,0)
∵△AOC的面积为1,
∴A(-1,1)
将A(-1,1)代入 ,
, 可得m=-1,n=-1;
可得m=-1,n=-1;
(2)设直线AC的解析式为y=kx+b
∵y=kx+b经过点A(-1,1)、C(1,0)
∴ 解得k=-
解得k=- ,b=
,b= .
.
∴直线AC的解析式为y=- x+
x+ .
.
考点:一次函数与反比例函数图象的交点问题
点评:此类问题是初中数学的重点,在中考中极为常见,熟练掌握待定系数法是解题关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.
是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.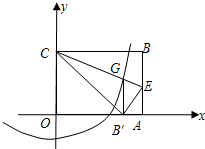 半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标. 已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.
已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D. 如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.
如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.