题目内容
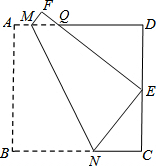
如图,将边长为2的正方形纸片ABCD折叠,使点B落在CD上,落点记为E(不与点C,D重合),点A落在点F处,折痕MN交AD于点M,交BC于点N.若
=
,则BN的长是______,
的值等于______;若
=
(n≥2,且n为整数),则
的值等于______(用含n的式子表示).

| CE |
| CD |
| 1 |
| 2 |
| AM |
| BN |
| CE |
| CD |
| 1 |
| n |
| AM |
| BN |

∵沿MN折叠B和E重合,
∴BN=NE,
∵
=
,CD=2,
∴CE=1,
设BN=NE=x
在Rt△CEN中,由勾股定理得:NE2=CE2+CN2,
x2=12+(2-x)2
x=
,
BN=NE=
.
∵四边形ABCD是正方形,
∴∠A=∠C=∠D=90°,
∴∠QEN=∠B=90°,
∴∠DQE+∠DEQ=∠CEN+∠DEQ=90°,
∴∠DQE=∠CEN,
∵∠D=∠C=90°,
∴△DQE∽△CEN,
∴
=
=
,
∴
=
=
,
DQ=
,EQ=
,
∵折叠A和F重合,B和E重合,
∴∠F=∠A=90°,EF=AB=2,AM=MF,
在Rt△MFQ中,由勾股定理得:MQ2=MF2+FQ2,
(2-
-AM)2=AM2+(2-
)2,
AM=
.
∵沿MN折叠B和E重合,
∴BN=NE,
∵
=
,CD=2,
∴CE=
,
设BN=NE=x
在Rt△CEN中,由勾股定理得:NE2=CE2+CN2,
x2=(
)2+(2-x)2
x=
,
BN=NE=
.
∵四边形ABCD是正方形,
∴∠A=∠C=∠D=90°,
∴∠QEN=∠B=90°,
∴∠DQE+∠DEQ=∠CEN+∠DEQ=90°,
∴∠DQE=∠CEN,
∵∠D=∠C=90°,
∴△DQE∽△CEN,
∴
=
=
,
∴
=
=
,
DQ=
,EQ=
,
∵折叠A和F重合,B和E重合,
∴∠F=∠A=90°,EF=AB=2,AM=MF,
在Rt△MFQ中,由勾股定理得:MQ2=MF2+FQ2,
(2-
-AM)2=AM2+(2-
)2,
AM=
,
∴
=
,
故答案为:
,
,
.
∴BN=NE,
∵
| CE |
| CD |
| 1 |
| 2 |
∴CE=1,
设BN=NE=x
在Rt△CEN中,由勾股定理得:NE2=CE2+CN2,
x2=12+(2-x)2
x=
| 5 |
| 4 |
BN=NE=
| 5 |
| 4 |

∵四边形ABCD是正方形,
∴∠A=∠C=∠D=90°,
∴∠QEN=∠B=90°,
∴∠DQE+∠DEQ=∠CEN+∠DEQ=90°,
∴∠DQE=∠CEN,
∵∠D=∠C=90°,
∴△DQE∽△CEN,
∴
| CE |
| DQ |
| EN |
| QE |
| CN |
| DE |
∴
| 1 |
| DQ |
| ||
| EQ |
2-
| ||
| 2-1 |
DQ=
| 4 |
| 3 |
| 5 |
| 3 |
∵折叠A和F重合,B和E重合,
∴∠F=∠A=90°,EF=AB=2,AM=MF,
在Rt△MFQ中,由勾股定理得:MQ2=MF2+FQ2,
(2-
| 4 |
| 3 |
| 5 |
| 3 |
AM=
| 1 |
| 4 |
∵沿MN折叠B和E重合,
∴BN=NE,
∵
| CE |
| CD |
| 1 |
| n |
∴CE=
| 2 |
| n |
设BN=NE=x
在Rt△CEN中,由勾股定理得:NE2=CE2+CN2,
x2=(
| 2 |
| n |
x=
| 1+n2 |
| n2 |
BN=NE=
| 1+n2 |
| n2 |
∵四边形ABCD是正方形,
∴∠A=∠C=∠D=90°,
∴∠QEN=∠B=90°,
∴∠DQE+∠DEQ=∠CEN+∠DEQ=90°,
∴∠DQE=∠CEN,
∵∠D=∠C=90°,
∴△DQE∽△CEN,
∴
| CE |
| DQ |
| EN |
| QE |
| CN |
| DE |
∴
| ||
| DQ |
| ||
| EQ |
2-
| ||
2-
|
DQ=
| 4 |
| n+1 |
| 2+2n2 |
| n2+n |
∵折叠A和F重合,B和E重合,
∴∠F=∠A=90°,EF=AB=2,AM=MF,
在Rt△MFQ中,由勾股定理得:MQ2=MF2+FQ2,
(2-
| 4 |
| n+1 |
| 2+2n2 |
| n2+n |
AM=
| (n-1)2 |
| n2 |
∴
| AM |
| BN |
| (n-1)2 |
| n2+1 |
故答案为:
| 5 |
| 4 |
| 1 |
| 5 |
| (n-1)2 |
| n2+1 |

练习册系列答案
相关题目
 ,求△ABC的面积.
,求△ABC的面积. 的格点△DEF;
的格点△DEF;  ,
,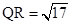 ,则六边形AQRDEF的面积为__________.
,则六边形AQRDEF的面积为__________.