题目内容
平面直角坐标系中,O是坐标原点.直线y=kx+b(k≠0)经过点A(1,2),与x轴交于点M,与y轴交于点N.若OA2=AM•AN,则点M的坐标是________.
(5,0)、(-3,0),(0,0)、(2,0)
分析:把A的坐标代入直线的解析式求出y=(2-b)x+b,求出M、N的坐标,根据已知和勾股定理得到25=[4+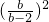 ]×[1+(b-2)2],求出方程的解即可
]×[1+(b-2)2],求出方程的解即可
解答:把A(1,2)代入y=kx+b得:2=k+b,
∴k=2-b,
∴y=(2-b)x+b,
当x=0时y=b,
当y=0时,x=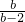 ,
,
∴N(0,b),M(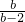 ,0),
,0),
∵OA2=AM•AN,
∴OA4=AN2•AM2,
由勾股定理得:OA= =
= ,
,
25=[4+ ]×[1+(b-2)2],
]×[1+(b-2)2],
25=[4+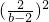 ]×[1+(b-2)2],
]×[1+(b-2)2],
25=4+4(b-2)2+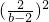 +4,
+4,
即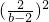 +4(b-2)2-17=0,
+4(b-2)2-17=0,
解得:b1= ,b2=
,b2= ,b3=4,b4=0,
,b3=4,b4=0,
∴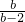 的值是5或-3或2或0,
的值是5或-3或2或0,
∴M的坐标是(5,0),(-3,0),(2,0),(0,0),
故答案为:(5,0),(-3,0),(2,0),(0,0).
点评:本题主要考查对勾股定理,一次函数图象上点的坐标特征等知识点的理解和掌握,综合运用性质进行计算是解此题的关键.
分析:把A的坐标代入直线的解析式求出y=(2-b)x+b,求出M、N的坐标,根据已知和勾股定理得到25=[4+
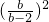 ]×[1+(b-2)2],求出方程的解即可
]×[1+(b-2)2],求出方程的解即可解答:把A(1,2)代入y=kx+b得:2=k+b,
∴k=2-b,
∴y=(2-b)x+b,
当x=0时y=b,
当y=0时,x=
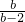 ,
,∴N(0,b),M(
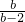 ,0),
,0),∵OA2=AM•AN,
∴OA4=AN2•AM2,
由勾股定理得:OA=
 =
= ,
,25=[4+
 ]×[1+(b-2)2],
]×[1+(b-2)2],25=[4+
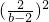 ]×[1+(b-2)2],
]×[1+(b-2)2],25=4+4(b-2)2+
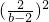 +4,
+4,即
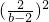 +4(b-2)2-17=0,
+4(b-2)2-17=0,解得:b1=
 ,b2=
,b2= ,b3=4,b4=0,
,b3=4,b4=0,∴
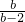 的值是5或-3或2或0,
的值是5或-3或2或0,∴M的坐标是(5,0),(-3,0),(2,0),(0,0),
故答案为:(5,0),(-3,0),(2,0),(0,0).
点评:本题主要考查对勾股定理,一次函数图象上点的坐标特征等知识点的理解和掌握,综合运用性质进行计算是解此题的关键.

练习册系列答案
相关题目
 形BEFG是否存在邻边相等的情况?若存在,请直接写出此时m的值,并指出相等的邻边;若不存在,说明理由.
形BEFG是否存在邻边相等的情况?若存在,请直接写出此时m的值,并指出相等的邻边;若不存在,说明理由. 如图,在平面直角坐标系中,以O(0,0),A(1,1),B(3,0)为顶点,构造平行四边形,则第四个顶点的坐标可以是
如图,在平面直角坐标系中,以O(0,0),A(1,1),B(3,0)为顶点,构造平行四边形,则第四个顶点的坐标可以是