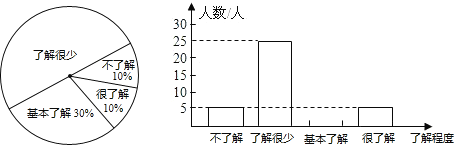
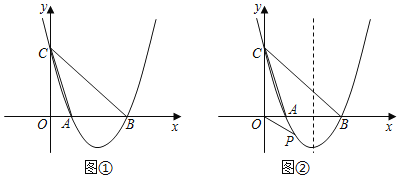
��Ŀ����
����Ŀ�����������������֪����ͬ����Ȼ����Ե�Բ�ܽǶ���ȣ��ҵ������������Ե�Բ�Ľǵ�һ�룮��ô����һ��Բ��ͬһ�������Ե�Բ�ܽ���Բ�Ľ�֮������ʲô��ϵ��
������˼������1����ͼ��![]() ��
��![]() ���ң�
���ң�![]() ����
����![]() ��
��![]() �ֱ����Ż�
�ֱ����Ż�![]() ���ӻ�
���ӻ�![]() �ϵĵ㣬��
�ϵĵ㣬��![]() ______����
______����![]() _______����
_______����

��2����ͼ��![]() ��
��![]() ���ң�Բ�Ľ�
���ң�Բ�Ľ�![]() ����P��
����P��![]() �ϲ���A��B�غϵ�һ�㣬����
�ϲ���A��B�غϵ�һ�㣬����![]() ���Ե�Բ�ܽ�
���Ե�Բ�ܽ�![]() �Ķ�������m�Ĵ���ʽ��ʾ����
�Ķ�������m�Ĵ���ʽ��ʾ����

������������3����ͼ����֪�߶�![]() ����C��
����C��![]() ����ֱ�ߵ��Ϸ�����
����ֱ�ߵ��Ϸ�����![]() ���ó߹���ͼ�ķ����������������ĵ�C����ɵ�ͼ�Σ���д������������ͼ�ۼ�����
���ó߹���ͼ�ķ����������������ĵ�C����ɵ�ͼ�Σ���д������������ͼ�ۼ�����
![]()
���𰸡���1����1��50����130������2��![]() ����3��������
����3��������
��������
��1������ͬ����Ȼ����Ե�Բ�ܽǶ���ȣ��ҵ������������Ե�Բ�Ľǵ�һ�룬���ɵý⣻
��2�����Ƚ���P��������ۣ��Ż����ӻ���Ȼ��ֱ�Ӹ���ͬ����Ȼ����Ե�Բ�ܽǶ���ȣ��ҵ������������Ե�Բ�Ľǵ�һ�룬���ɵý⣻
��3�����ݣ�2�������ý��ۣ���AB���е�ΪԲ�ģ�ABΪֱ����Բ��Ȼ���Բ�������䴹ֱ��ֱ������Բ��D��E���㣬����DΪԲ�ģ�DBΪ�뾶��Բ���ӻ�AB��Ϊ����.
��1���������⣬��
![]() ��
��
![]()
��2����P���Ż�![]() ��ʱ
��ʱ![]()
��![]() ���ӻ�
���ӻ�![]() ��ʱ��
��ʱ��![]() ��
��
��![]()
��3����ͼ��ʾ��

��ͼ��Ϊ�����ӻ�![]() ����
����