题目内容
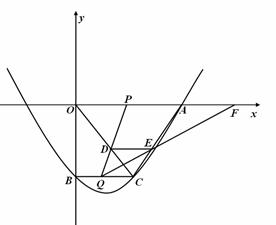
如图,在平面直角坐标系xoy中,抛物线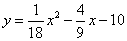 与x轴,y轴的交点分别为点A,点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
与x轴,y轴的交点分别为点A,点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
(1)求A,B,C三点的坐标和抛物线的顶点的坐标;
(2)当t为何值时,四边形PQCA为平行四边形?请写出计算过程;
(3)当0<t<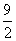 时,△PQF的面积是否总为定值?若是,求出此定值,若不是,请说明理由;
时,△PQF的面积是否总为定值?若是,求出此定值,若不是,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?请写出解答过程.
解:(1) ,令
,令 得
得 ,
,
∴ 或
或 ∴
∴ ;
;
在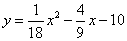 中,令
中,令 得
得 即
即 ;
;
由于BC∥OA,故点C的纵坐标为-10,由 得
得 或
或
即 且易求出顶点坐标为
且易求出顶点坐标为
于是, ,顶点坐标为
,顶点坐标为 。
。
(2)若四边形PQCA为平行四边形,由于QC∥PA。故只要QC=PA即可,而 故
故 得
得 ;
;
(3)设点P运动 秒,则
秒,则 ,
, ,说明P在线段OA上,且不与点OA、重合,
,说明P在线段OA上,且不与点OA、重合,
由于QC∥OP知△QDC∽△PDO,故
∴ ∴
∴
又点Q到直线PF的距离 ,∴
,∴ ,
,
于是△PQF的面积总为90。
(4)由上知, ,
, 。构造直角三角形后易得
。构造直角三角形后易得


① 若FP=PQ,即 ,故
,故 ,
,
∵ ∴
∴ ∴
∴
② 若QP=QF,即 ,无
,无 的
的 满足条件;
满足条件;
③ 若PQ=PF,即 ,得
,得 ,∴
,∴ 或
或 都不满足
都不满足 ,故无
,故无 的
的 满足方程;
满足方程;
综上所述:当 时,△PQR是等腰三角形。
时,△PQR是等腰三角形。

不等式组 的解集是( )
的解集是( )
|
| A. | x>2 | B. | x>1 | C. | 1<x<2 | D. | 无解 |
如图所示,几何体的主视图是( )

|
| A. |
| B. |
| C. |
| D. |
|
某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某校初中生阅读数学教科书情况统计图表
| 类别 | 人数 | 占总人数比例 |
| 重视 | a | 0.3 |
| 一般 | 57 | 0.38 |
| 不重视 | b | c |
| 说不清楚 | 9 | 0.06 |
(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2300名,请估计该校“不重视阅读数学教科书”的初中人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?

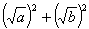 =
=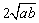 +
+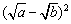 +
+ 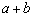 ≥
≥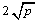 ,当且仅当a、b满足 时,a+b有最小值
,当且仅当a、b满足 时,a+b有最小值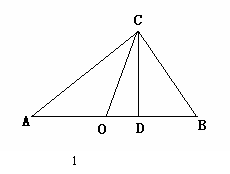
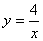 的图像上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连结DF、EF,求四边形ADFE面积的最小值.
的图像上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连结DF、EF,求四边形ADFE面积的最小值.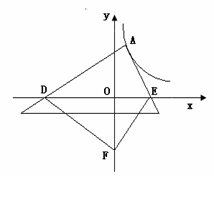

 的范围内选取一个合适的整数
的范围内选取一个合适的整数 代入求值.
代入求值. 的倒数是 ,写出一个比-3大而比-2小的无理数是 .
的倒数是 ,写出一个比-3大而比-2小的无理数是 .