题目内容
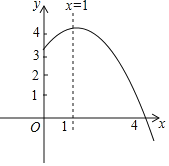
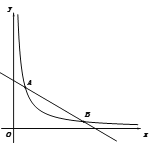
【题目】如图，已知一次函数y＝－
x＋b与反比例函数y＝
（x＞0）的图象交于点A（2，6）和点B（m，1）
（1）求一次函数和反比例函数的解析式；
（2）点E为y轴上一个动点，若S△AEB＝5，求点E的坐标．
【答案】（1）y=-
x+7，y=
(x>0)；（2）点E的坐标为（0，6）或（0，8）．
【解析】
（1）把点A的坐标代入y
，求出反比例函数的解析式，把点B的坐标代入反比例函数，得出点B的坐标，再把A的坐标代入直线y
x+b，求出b的值，从而得出一次函数的解析式；
（2）设直线AB与y轴的交点为P，点E的坐标为（0，a），连接AE，BE，先求出点P的坐标（0，7），得出PE=|a﹣7|，根据S△AEB=S△BEP﹣S△AEP=5，求出a的值，从而得出点E的坐标．
（1）把点A（2，6）代入y，得：k=12，则y
．
把点B（m，1）代入y，得：m=12，则点B的坐标为（12，1）．
由直线yx+b过点A（2，6），得： 6
2+b，解得：b=7，则所求一次函数的表达式为yx+7．
（2）如图，设直线AB与y轴的交点为P，点E的坐标为（0，a），连接AE，BE，则点P的坐标为（0，7），∴PE=|a﹣7|．
∵S△AEB=S△BEP﹣S△AEP=5，∴
|a﹣7|×（12﹣2）=5，∴|a﹣7|=1，∴a1=6，a2=8，∴点E的坐标为（0，6）或（0，8）．
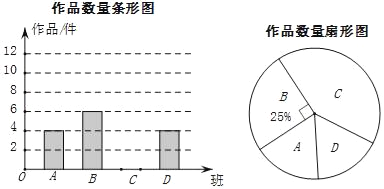
阅读快车系列答案【题目】为了了解学生关注热点新闻的情况，“两会”期间，小明对班级同学一周内收看“两会”新闻的次数情况作了调查，调查结果统计如图所示（其中男生收看
次的人数没有标出）.
根据上述信息，解答下列各题：
×
（1）该班级女生人数是__________，女生收看“两会”新闻次数的中位数是________；
（2）对于某个群体，我们把一周内收看某热点新闻次数不低于次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低
，试求该班级男生人数；
（3）为进一步分析该班级男、女生收看“两会”新闻次数的特点，小明给出了男生的部分统计量（如表）.
统计量 | 平均数（次） | 中位数（次） | 众数（次） | 方差 | … |
该班级男生 |
|
|
|
| … |
根据你所学过的统计知识，适当计算女生的有关统计量，进而比较该班级男、女生收看“两会”新闻次数的波动大小.
