题目内容
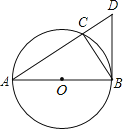
【题目】如图,⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D。
(1)求证:△ABC∽△BDC。
(2)若AC=8,BC=6,求△BDC的面积。
【答案】(1)答案见解析 (2) ![]()
【解析】【试题分析】(1)根据切线的性质和直径所对的圆周角是直角,得∠ACB=∠BCD=90°,根据同角的余角相等,得∠A=∠CBD;根据两角对应相等,两三角形相似得,△ABC∽△BDC;(2)根据相似三角形的对应边成比例,得![]() =
=![]() ,即
,即![]() =
=![]() ,解得DC=
,解得DC=![]() ,可得
,可得![]() =
=![]() BC·DC=
BC·DC=![]() ×6×
×6×![]() =
=![]() ;
;
【试题解析】
(1)∵BD是切线,圆心O在AB上,
∴BD⊥AB,∠ABC=90°,
∴∠ACB=∠BCD=90°,
∵∠ABC+∠A=90°,∠CBD+∠ABC=90°,
∴∠A=∠CBD,
∴△ABC∽△BDC;
(2)∵△ABC∽△BDC,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴DC=![]() ,
,
∴![]() =
=![]() BC·DC,
BC·DC,
=![]() ×6×
×6×![]() ,
,
=![]() ;
;

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目