题目内容
【题目】在平面直角坐标系![]() 中,对于任意一点
中,对于任意一点![]() ,定义点
,定义点![]() 的“离心值”
的“离心值”![]() 为:
为: 时,例如对于点
时,例如对于点![]() ,因为
,因为![]() ,所以
,所以![]() .
.
解决下列问题:
(1)已知![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的值,并将
的值,并将![]() ,
,![]() ,
,![]() 按从小到大的顺序排列(用“<”连接);
按从小到大的顺序排列(用“<”连接);
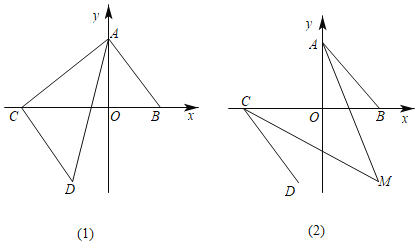
(2)如图,点![]() ,线段
,线段![]() 上的点
上的点![]() ,
,
①若![]() ,求点
,求点![]() 的坐标;
的坐标;
②在图中画出满足![]() 的点
的点![]() 组成的图形,并用语言描述该图形的特征;
组成的图形,并用语言描述该图形的特征;

【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ,
,![]() ;②见解析.
;②见解析.
【解析】
(1)根据“离心值”的定义求解即可;
(2)①由题意得,点P,点Q在直线x=-![]() 上,再根据“离心值”的定义求出y的值,即可确定P、Q的坐标;
上,再根据“离心值”的定义求出y的值,即可确定P、Q的坐标;
②根据“离心值”的定义,求出M的坐标,根据图形进行描述即可.
(1)∵|-![]() |>|-1|
|>|-1|
∴![]() =|-
=|-![]() |=
|=![]() ;
;
∵|0|<|5|,
∴![]() =5,
=5,
∵|-3|=3,
∴![]() =3,
=3,
∴![]()
(2)①∵点![]()
∴![]() ,且线段
,且线段![]() 轴
轴
对于线段![]() 上的点
上的点![]() ,它的横坐标
,它的横坐标![]() ,纵坐标
,纵坐标![]() 满足
满足![]()
∴线段![]() 上满足
上满足![]() 的点
的点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
②根据离心值的定义可知,满足![]() 的点
的点![]() 组成的图形如图所示,
组成的图形如图所示,
该图形是线段![]() ,其中
,其中![]()


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目