题目内容
如图在△ABC中，M是BC中点，AP是∠A平分线，BP⊥AP于P，AB=12，AC=22，则MP长为（ ）| A、3 | B、4 | C、5 | D、6 |
分析：延长BP交AC于N，利用角边角定理求证△ABP≌△ANP，再利用M是BC中点，求证PM是△BNC的中位线，即可求出MP的长．
解答：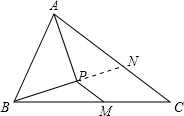
解：延长BP交AC于N
∵AP是∠BAC的角平分线，BP⊥AP于P，
∴∠BAP=∠NAP，∠APB=∠APN=90°，
∴△ABP≌△ANP（ASA），
∴AN=AB=12，BP=PN，
∴CN=AC-AN=22-12=10，
∵BP=PN，BM=CM，
∴PM是△BNC的中位线，
∴PM=
CN=5．
故选C．
解：延长BP交AC于N∵AP是∠BAC的角平分线，BP⊥AP于P，
∴∠BAP=∠NAP，∠APB=∠APN=90°，
∴△ABP≌△ANP（ASA），
∴AN=AB=12，BP=PN，
∴CN=AC-AN=22-12=10，
∵BP=PN，BM=CM，
∴PM是△BNC的中位线，
∴PM=
| 1 |
| 2 |
故选C．
点评：此题主要考查学生对全等三角形的判定与性质和三角形中位线定理的理解和掌握，解答此题的关键是求证PM是△BNC的中位线．
练习册系列答案
走进文言文系列答案
相关题目
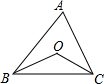如图在△ABC中，∠ABC=50°，∠ACB=75°，点O是内心，则∠BOC的度数为
如图在△ABC中，∠A=45°，tanB=3，BC=
已知，如图在△ABC中，AD是BC边上的高线，CE是AB边上的中线，DG平分∠CDE，DC=AE，
如图在△ABC中，AD垂直平分BC，AD=8，BC=10，E、F是AD上的两点，则图中阴影部分的面积是