题目内容
问题提出:我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一,所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N。
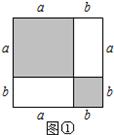
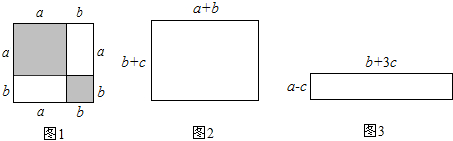
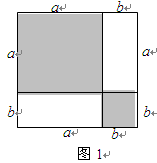
问题解决:如图1,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形面积之和M与两个矩形面积之和N的大小。
解:由图可知:M=a2+b2,N=2ab,
∴M-N=a2+b2-2ab=(a-b)2,
∵a≠b,
∴(a-b)2>0,
∴M-N>0,
∴M>N。
问题解决:如图1,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形面积之和M与两个矩形面积之和N的大小。
解:由图可知:M=a2+b2,N=2ab,
∴M-N=a2+b2-2ab=(a-b)2,
∵a≠b,
∴(a-b)2>0,
∴M-N>0,
∴M>N。
类别应用:
(1)已知小丽和小颖购买同一种商品的平均价格分别为 元/千克和
元/千克和 元/千克(a、b是正数,且a≠b),试比较小丽和小颖所购买商品的平均价格的高低。
元/千克(a、b是正数,且a≠b),试比较小丽和小颖所购买商品的平均价格的高低。
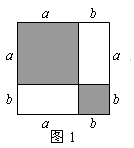
(2)试比较图2和图3中两个矩形周长M1、N1的大小(b>c)。
(1)已知小丽和小颖购买同一种商品的平均价格分别为
 元/千克和
元/千克和 元/千克(a、b是正数,且a≠b),试比较小丽和小颖所购买商品的平均价格的高低。
元/千克(a、b是正数,且a≠b),试比较小丽和小颖所购买商品的平均价格的高低。(2)试比较图2和图3中两个矩形周长M1、N1的大小(b>c)。


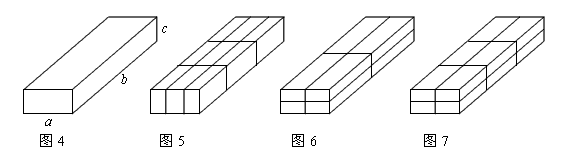
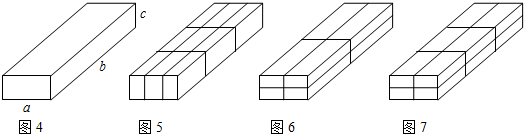
联系拓广:小刚在超市里买了一些物品,用一个长方体的箱子“打包”,这个箱子的尺寸如图4所示(其中b>a>c>0),售货员分别可按图5、图6、图7三种方法进行捆绑,问哪种方法用绳最短?哪种方法用绳最长?请说明理由。
解:类别应用:(1)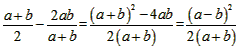 ,
,
∵a,b是正整数且a≠b,
∴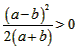 ,
,
∴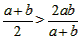 ,
,
∴小丽购买商品的平均价格比小颖的高;
(2)由图知,M1=2(a+b+b+c)=2a+4b+2c,
N1=2(a-c+b+3c)=2a+2b+4c,
M1-N1=(2a+4b+2c)-(2a+2b+4c)=2b-2c=2(b-c)
∵b>c,
∴M1-N1=2(b-c)>0,即M1>N1,
所以第一个矩形的周长大于第二个矩形的周长;
联系拓广:设图5的捆绑绳长为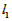 ,则
,则 =2a×2b+2×2+4c×2=4a+4b+8c
=2a×2b+2×2+4c×2=4a+4b+8c
设图6的捆绑绳长为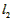 ,则
,则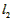 =2a×2+2b×2+2c×2=4a+4b+4c
=2a×2+2b×2+2c×2=4a+4b+4c
设图7的捆绑绳长为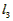 ,则
,则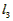 =3a×2+2b×2+3c×2=6a+4b+6c
=3a×2+2b×2+3c×2=6a+4b+6c
∵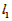 -
-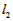 =(4a+4b+8c)-(4a+4b+4c)=4c>0,
=(4a+4b+8c)-(4a+4b+4c)=4c>0,
∴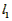 >
>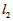 ,
,
∵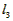 -
-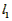 =(6a+4b+6c)-(4a+4b+8c)=2a-2c>0,
=(6a+4b+6c)-(4a+4b+8c)=2a-2c>0,
=2(a-c)>0,(∵已知a>c)
∴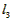 >
>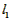 ,
,
∴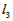 >
>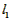 >
>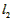 ,
,
所以第三种捆绑方法用绳最长,第二种最短。
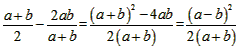 ,
,∵a,b是正整数且a≠b,
∴
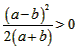 ,
,∴
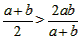 ,
,∴小丽购买商品的平均价格比小颖的高;
(2)由图知,M1=2(a+b+b+c)=2a+4b+2c,
N1=2(a-c+b+3c)=2a+2b+4c,
M1-N1=(2a+4b+2c)-(2a+2b+4c)=2b-2c=2(b-c)
∵b>c,
∴M1-N1=2(b-c)>0,即M1>N1,
所以第一个矩形的周长大于第二个矩形的周长;
联系拓广:设图5的捆绑绳长为
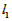 ,则
,则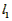 =2a×2b+2×2+4c×2=4a+4b+8c
=2a×2b+2×2+4c×2=4a+4b+8c设图6的捆绑绳长为
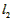 ,则
,则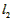 =2a×2+2b×2+2c×2=4a+4b+4c
=2a×2+2b×2+2c×2=4a+4b+4c 设图7的捆绑绳长为
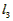 ,则
,则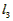 =3a×2+2b×2+3c×2=6a+4b+6c
=3a×2+2b×2+3c×2=6a+4b+6c∵
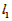 -
-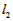 =(4a+4b+8c)-(4a+4b+4c)=4c>0,
=(4a+4b+8c)-(4a+4b+4c)=4c>0, ∴
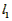 >
>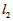 ,
,∵
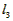 -
-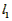 =(6a+4b+6c)-(4a+4b+8c)=2a-2c>0,
=(6a+4b+6c)-(4a+4b+8c)=2a-2c>0, =2(a-c)>0,(∵已知a>c)
∴
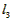 >
>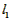 ,
,∴
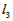 >
>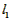 >
>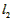 ,
,所以第三种捆绑方法用绳最长,第二种最短。

练习册系列答案
相关题目
 ,
, .
. .
. >0.
>0.


 ,
, .
. .
.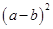 >0.
>0.

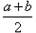 元/千克、
元/千克、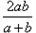 元/千克(a·b是正数.且a≠b),试比较小丽和小颖所购商品的平均价格的高低.
元/千克(a·b是正数.且a≠b),试比较小丽和小颖所购商品的平均价格的高低.