题目内容
【题目】操作探究:
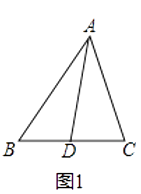
(1)实践:如图1, ![]() 中,
中,![]() 为
为![]() 边上的中线,
边上的中线,![]() 的面积记为
的面积记为![]() ,
,![]() 的面积记为
的面积记为![]() .则
.则![]() .
.

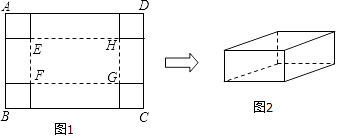
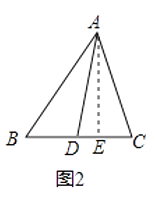
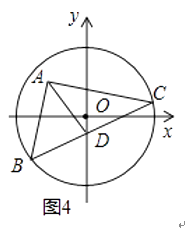
(2)探究:在图2中,![]() 、
、![]() 分别为四边形
分别为四边形![]() 的边
的边![]() 、
、![]() 的中点,四边形
的中点,四边形![]() 的面积记为
的面积记为![]() ,阴影部分面积记为
,阴影部分面积记为![]() ,则
,则![]() 和
和![]() 之间满足的关系式为______:
之间满足的关系式为______:
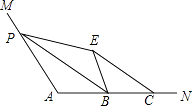
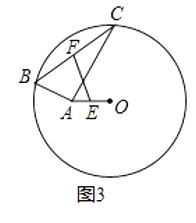
(3)解决问题:
在图3中,![]() 、
、![]() 、
、![]() 、
、![]() 分别为任意四边形
分别为任意四边形![]() 的边
的边![]() 、
、![]() 、
、![]() 、
、![]() 的中点,并且图中阴影部分的面积为
的中点,并且图中阴影部分的面积为![]() 平方厘米,求图中四个小三角形的面积和,并说明理由.
平方厘米,求图中四个小三角形的面积和,并说明理由.
【答案】(2)S阴=![]() S四边形ABCD;(3)20,证明见解析
S四边形ABCD;(3)20,证明见解析
【解析】
(2)利用E、F分别为任意四边形ABCD的边AD、BC的中点,分别求得则S阴和S四边形ABCD即可.
(3)先设空白处面积分别为:x、y、m、n,由上得 S四边形BEDF=![]() S四边形ABCD,S四边形AHCG=
S四边形ABCD,S四边形AHCG=![]() S四边形ABCD,可得(S1+x+S2+S3+y+S4)+(S1+m+S4+S2+n+S3)=S1+x+S2+n+S3+y+S4+m+S阴,然后S1+S2+S3+S4=S阴即可.
S四边形ABCD,可得(S1+x+S2+S3+y+S4)+(S1+m+S4+S2+n+S3)=S1+x+S2+n+S3+y+S4+m+S阴,然后S1+S2+S3+S4=S阴即可.
(2)由E、F分别为矩形ABCD的边AD、BC的中点,
得S阴=BFCD=![]() BCCD,
BCCD,
S四边形ABCD=BCCD,
所以S阴=![]() S四边形ABCD;
S四边形ABCD;
(3)设空白处面积分别为:x、y、m、n,由题意得
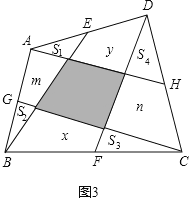
S四边形BEDF=![]() S四边形ABCD,S四边形AHCG=
S四边形ABCD,S四边形AHCG=![]() S四边形ABCD,
S四边形ABCD,
∴S1+x+S2+S3+y+S4=![]() S四边形ABCD,S1+m+S4+S2+n+S3=
S四边形ABCD,S1+m+S4+S2+n+S3=![]() S四边形ABCD,
S四边形ABCD,
∴(S1+x+S2+S3+y+S4)+(S1+m+S4+S2+n+S3)=S四边形ABCD.
∴(S1+x+S2+S3+y+S4)+(S1+m+S4+S2+n+S3)=S1+x+S2+n+S3+y+S4+m+S阴,
∴S1+S2+S3+S4=S阴=20平方厘米.
故四个小三角形的面积和为20平方厘米.

练习册系列答案
相关题目