��Ŀ����
����Ŀ�������������⣺
�ٺ���![]() ��ż�������������溯����
��ż�������������溯����
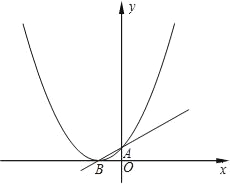
����֪�ع�ֱ�߷���Ϊ![]() �������������Ϊ
�������������Ϊ![]() ����
����![]() ��
��
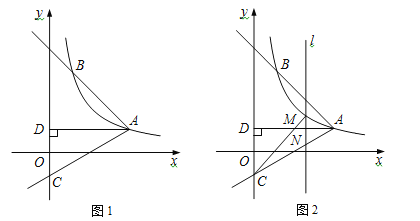
�ۺ���![]() ͼ����ڵ�
ͼ����ڵ�![]() �Գ�����
�Գ�����![]() �ϵ���������
�ϵ���������
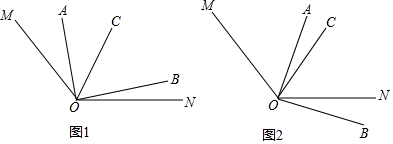
�ܸ��ݵ����������������ƶ��Ҫ������ijũҵ���ò��ž����ɳ���λ���ר�Ҷ�����ƶ���������е��У�ÿ������������Dzһλר�ң����мס�����λר����Ҫ��Dz��ͬһ��������ͬ����Dz����������![]() �֣�
�֣�
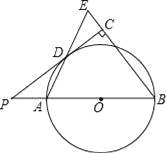
����֪˫����![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ����
����![]() ��ֱ�߽�˫������֧��
��ֱ�߽�˫������֧��![]() ���㣬��
���㣬��![]() ����
����![]() ����˫���ߵ�������Ϊ
����˫���ߵ�������Ϊ![]() .
.
������ȷ���������Ϊ_____.
���𰸡��ڢۢ�
��������
������������Ķ�������������Ľ���ʽ��������ż�ԵĶ��弴���жϢ٣����ݻع�ֱ�߹��������ĵ㣬���뼴���жϢڣ��������Һ��������ʣ�������֤��������뼴���жϢۣ����÷������ԭ���Լ�����������жϢܣ�����˫���ߵĶ����Լ������ʹ�ʽ�����жϢ�.
�ٺ����Ķ�����Ϊ![]() ��
��![]() �������溯������ż�������ʴ���
�������溯������ż�������ʴ���
�ڸ��ݻع�ֱ�߷��̺�����������ĵ㣬��![]() ����ع鷽�̿ɵ�
����ع鷽�̿ɵ�![]() ������ȷ��
������ȷ��
�۰�![]() ���뺯��
���뺯��![]() ������ֵΪ
������ֵΪ![]() �����Ժ���
�����Ժ���![]() ����
����![]() �Գƣ���
�Գƣ���![]() ���ɵú���
���ɵú���![]() �ĵ�����������Ϊ
�ĵ�����������Ϊ![]() �����Ժ���
�����Ժ���![]() ��
��![]() ���ǵ�����.����ȷ��
���ǵ�����.����ȷ��
�ܸ������⣬��![]() ��������ۣ���һ�֣�
��������ۣ���һ�֣�![]() �˷ֳ�
�˷ֳ�![]() �����飬
�����飬
������![]() �˷ֵ�ͬһ����������
�˷ֵ�ͬһ����������![]() ����������ѡ
����������ѡ![]() �������ż��ң���
�������ż��ң���![]() �������
�������
��ʣ�µ�![]() �˷ֳ�
�˷ֳ�![]() �飬��
�飬��![]() �ַ��鷽������
�ַ��鷽������![]() ��ȫ���У����ŵ�����
��ȫ���У����ŵ�����![]() ��������
��������
��![]() ����������ʱ��
����������ʱ��![]() �ְ��ŷ�����
�ְ��ŷ�����
�ڶ��֣�![]() �˷ֳ�
�˷ֳ�![]() �����飬���������������е�
�����飬���������������е�![]() �ˣ�һ���ŵ�ͬһ������
�ˣ�һ���ŵ�ͬһ������
������![]() ������ѡ
������ѡ![]() �ˣ������һ���ŵ�һ����������
�ˣ������һ���ŵ�һ����������![]()
![]() �������
�������
��ʣ�µ�![]() ��ȫ���У����ŵ�����
��ȫ���У����ŵ�����![]() ����������
����������![]() �������
�������
���ʱ��![]() �ְ��ŷ�������һ����
�ְ��ŷ�������һ����![]() �ְ��ŷ���.�ʴ���.
�ְ��ŷ���.�ʴ���.
����![]() Ϊ˫������֧��һ�㣬��
Ϊ˫������֧��һ�㣬��![]() ��
��![]() ��
��

��ֱ��������![]() �У�
��![]() ��
��
��˫���ߵĶ����֪��![]() ��
��
��![]() ������
������![]() ��
��
��Ϊ![]() ��
��
![]()
![]() �����
�����![]() .
.
![]()
![]() ��
��
�ɹ��ɶ����ɵã�![]() ����
����![]() .����ȷ.
.����ȷ.

 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�