题目内容
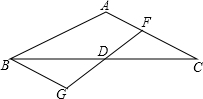 如图,△ABC中,AB=AC,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点.
如图,△ABC中,AB=AC,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点.(1)求证:BG=CF;
(2)请你判断AF、BG、AB之间的大小关系,并说明理由.
考点:全等三角形的判定与性质
专题:
分析:(1)由平行和中点,可证明△BGD≌△CFD,可得到BG=CF;
(2)结合(1)中的BG=CF,且AB=AC,可得到AF、BG、AB之间的关系.
(2)结合(1)中的BG=CF,且AB=AC,可得到AF、BG、AB之间的关系.
解答:证明:(1)∵AC∥BG,
∴∠GBD=∠C,
∵D是BC的中点,
∴BD=CD,
在△BGD和CFD中,
,
∴△BGD≌△CFD(ASA),
∴BG=CF;
(2)AB=AF+BG,理由如下:
由(1)可知:△BGD≌△CFD,
∴BG=FC,
∵AC=AF+FC,
∴AC=AF+BG,
∵AB=AC,
∴AB=AF+BG.
∴∠GBD=∠C,
∵D是BC的中点,
∴BD=CD,
在△BGD和CFD中,
|
∴△BGD≌△CFD(ASA),
∴BG=CF;
(2)AB=AF+BG,理由如下:
由(1)可知:△BGD≌△CFD,
∴BG=FC,
∵AC=AF+FC,
∴AC=AF+BG,
∵AB=AC,
∴AB=AF+BG.
点评:本题主要考查全等三角形的判定和性质,掌握全等三角形的判定和性质是解题的关键,证明三角形全等的方法有SSS、SAS、ASA、AAS和HL.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
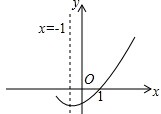 已知二次函数y=ax2+bx+c图象一部分,下面判断正确的有( )
已知二次函数y=ax2+bx+c图象一部分,下面判断正确的有( )| A、a+b+c=0 |
| B、b>2a |
| C、ax2+bx+c=0两根是-3和1 |
| D、a-2b+c>0 |
下列各式中结果为负数的是( )
| A、-(-3) |
| B、(-3)2 |
| C、|-3| |
| D、-|-3| |
在多项式x3-xy2+25中,最高次项是( )
| A、x3 |
| B、x3,xy2 |
| C、x3,-xy2 |
| D、25 |
已知a-b=1,则代数式a-b-3的值是( )
| A、4 | B、-4 | C、2 | D、-2 |
 如图,点A,B在数轴上,以AB为边作正方形,该正方形的面积是49.若点A对应的数是-2,则点B对应的数是( )
如图,点A,B在数轴上,以AB为边作正方形,该正方形的面积是49.若点A对应的数是-2,则点B对应的数是( ) 如图,一艘轮船从甲地向南偏西45°方向航行80km到达乙地后又向北航行100km到达丙地,这时它离甲地多远?(精确到1km)
如图,一艘轮船从甲地向南偏西45°方向航行80km到达乙地后又向北航行100km到达丙地,这时它离甲地多远?(精确到1km)