Question

如图，已知△ABC是边长为4的正三角形，AB在x轴上，点C在第一象限，AC与y轴交于点D，点A的坐标为（-1，0）．
（1）写出B，C，D三点的坐标；
（2）若抛物线y=ax²+bx+c经过B，C，D三点，求此抛物线的解析式．

Answer 1

解：（1）过C作CE⊥AB交x轴于E点，
∵△ABC是正三角形，AB=AC=BC=4，A（-1，0），
∴B（3，0），E（1，0），
∴AE=2，
在Rt△ACE中，CE==2，
∴C（1，2），
∵CE∥DO，
∴=，
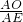∴DO=，
∴D（0，）；

（2）由抛物线y=ax²+bx+c经过B，C，D三点，
得：，
解得，
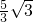∴抛物线的解析式为y=x²+x+．
分析：（1）过C作CE⊥ABxX轴于E点，可得出E的坐标，A、B的坐标，再由△ABC可求出CE的长度，继而可得出C的坐标，然后根据比例关系可求出D点坐标．
（2）用待定系数法求解，将三点代入联立求解可求出a、b、c的值，即得出函数解析式．
点评：本题考查待定系数法求二次函数解析式，结合了等边三角形的性质，综合性比较强，难度也很大．