题目内容
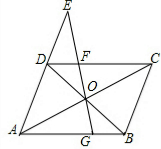 如图所示,?ABCD中,AC与BD交于O点,E为AD延长线上一点,OE交CD于F,EO延长线交AB于G.求证:
如图所示,?ABCD中,AC与BD交于O点,E为AD延长线上一点,OE交CD于F,EO延长线交AB于G.求证:| AB |
| DF |
| AD |
| DE |
分析:应利用平行四边形的性质,通过添加辅助线使各线段“集中”到一个三角形中来求证.
解答: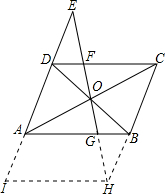 证明:延长CB与EG,其延长线交于H,如虚线所示,构造平行四边形AIHB.
证明:延长CB与EG,其延长线交于H,如虚线所示,构造平行四边形AIHB.
在△EIH中,由于DF∥IH,
∴
=
.
∵IH=AB,∴
=
,
从而,
-
=
-
=
=
=1+
.①
在△OED与△OBH中,
∠DOE=∠BOH,∠OED=∠OHB,OD=OB,
∴△OED≌△OBH(AAS).
从而DE=BH=AI,
∴
=1.②
由①,②得
-
=2.
 证明:延长CB与EG,其延长线交于H,如虚线所示,构造平行四边形AIHB.
证明:延长CB与EG,其延长线交于H,如虚线所示,构造平行四边形AIHB.在△EIH中,由于DF∥IH,
∴
| IH |
| DF |
| EI |
| ED |
∵IH=AB,∴
| AB |
| DF |
| EI |
| ED |
从而,
| AB |
| DF |
| AD |
| DE |
| EI |
| ED |
| AD |
| ED |
| EI-AD |
| ED |
| ED+AI |
| ED |
| AI |
| ED |
在△OED与△OBH中,
∠DOE=∠BOH,∠OED=∠OHB,OD=OB,
∴△OED≌△OBH(AAS).
从而DE=BH=AI,
∴
| AI |
| ED |
由①,②得
| AB |
| DF |
| AD |
| DE |
点评:此题考查学生对相似三角形的判定与性质和平行四边形的性质的理解和掌握,此题的关键是延长CB与EG,其延长线交于H,如虚线所示,构造平行四边形AIHB.这是此题的突破点,也是一个难点,因此属于一道难题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 34、如图所示,?ABCD的对角线AC和BD交于点O,若AC=6,BD=10,AB=4,则△AOB的周长等于
34、如图所示,?ABCD的对角线AC和BD交于点O,若AC=6,BD=10,AB=4,则△AOB的周长等于 38、如图所示,?ABCD中,M,N,P,Q分别为AB,BC,CD,DA上的点,且AM=BN=CP=DQ.
38、如图所示,?ABCD中,M,N,P,Q分别为AB,BC,CD,DA上的点,且AM=BN=CP=DQ.
 已知如图所示,?ABCD的对角线AC、BD交于O,GH过点O,分别交AD、BC于G、H,E、F在AC上且AE=CF,求证:四边形EHFG是平行四边形.
已知如图所示,?ABCD的对角线AC、BD交于O,GH过点O,分别交AD、BC于G、H,E、F在AC上且AE=CF,求证:四边形EHFG是平行四边形. 如图所示矩形ABCD中,已知点A(-3,3)、B(5,3)、C(5,-2),则点D的坐标为
如图所示矩形ABCD中,已知点A(-3,3)、B(5,3)、C(5,-2),则点D的坐标为