题目内容
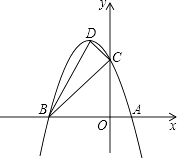
【题目】如图所示,已知抛物线C1、C2关于x轴对称,抛物线C1 , C3关于y轴对称,如果抛物线C2的解析式是y=﹣ ![]() (x﹣2)2+2,那么抛物线C3的解析式是( )
(x﹣2)2+2,那么抛物线C3的解析式是( ) 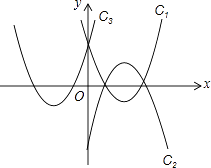
A.y=﹣ ![]() (x﹣2)2﹣2
(x﹣2)2﹣2
B.y=﹣ ![]() (x+2)2+2??
(x+2)2+2??
C.y= ![]() (x﹣2)2﹣2
(x﹣2)2﹣2
D.y= ![]() (x+2)2﹣2
(x+2)2﹣2
【答案】D
【解析】解:∵抛物线C1、C2关于x轴对称,且抛物线C2的解析式是y=﹣ ![]() (x﹣2)2+2, ∴抛物线C1的解析式是y=
(x﹣2)2+2, ∴抛物线C1的解析式是y= ![]() (x﹣2)2﹣2,
(x﹣2)2﹣2,
∵抛物线C1 , C3关于y轴对称,
∴抛物线C3的解析式是y= ![]() (﹣x﹣2)2﹣2=
(﹣x﹣2)2﹣2= ![]() (x+2)2﹣2.
(x+2)2﹣2.
故选D.
【考点精析】通过灵活运用二次函数图象的平移,掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减即可以解答此题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目