题目内容
已知△ABC中，AB=AC，∠A=36°，仿照图①，请你再设计两种不同的分法，将△ABC分割成3个三角形，使得每个三角形都是等腰三角形．
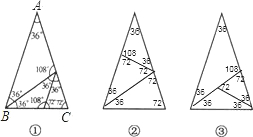解：如图，．
分析：利用三角形内角和定理和三角形外角性质以及提供的分法来作图．
点评：本题考查了等腰三角形的性质及三角形的内角和定理及三角形外角的性质；顶角为36°和108°的等腰三角形也是特殊的三角形，它可得到与它相似的三角形，主要是作底角的平分线．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
如图，已知△ABC中，AB=AC，AD平分∠BAC，请补充完整过程证明△ABD≌△ACD的理由．
已知△ABC中，AB=AC，AD为BC边上的中线，BE为AC边上的高，
如图，已知△ABC中，AB=AC，AD平分∠BAC，请补充完整过程，说明△ABD≌△ACD的理由．
如图：已知△ABC中，AB=17cm，BC=30cm，BC边上的中线AD=8cm．求证：△ABC是等腰三角形．