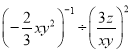��Ŀ����
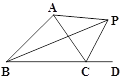
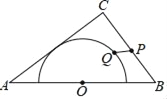
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬��A=30�㣬AB=8����P�ӵ�A������������AB��BC���յ�C�˶�����AB����ÿ��8����λ���ȵ��ٶ��˶�����BC����ÿ��2����λ���ȵ��ٶ��˶�����Q�ӵ�C��������CA������ÿ��![]() ����λ���ȵ��ٶ��˶�������ͬʱ����������Pֹͣʱ����QҲ��ֹ֮ͣ�����P�˶���ʱ��Ϊt�룮
����λ���ȵ��ٶ��˶�������ͬʱ����������Pֹͣʱ����QҲ��ֹ֮ͣ�����P�˶���ʱ��Ϊt�룮
��1�����߶�AQ�ij������ú�t�Ĵ���ʽ��ʾ��
��2������P��AB�����˶�ʱ����PQ���ABC��һ�ߴ�ֱʱt��ֵ��
��3�����APQ�����ΪS����S��t�ĺ�����ϵʽ��
��4������APQ����PQΪ���ĵ���������ʱ��ֱ��д��t��ֵ��
���𰸡���1��4![]() ��
��![]() t����2������P��AB�����˶�ʱ��PQ���ABC��һ�ߴ�ֱʱt��ֵ��t=0��
t����2������P��AB�����˶�ʱ��PQ���ABC��һ�ߴ�ֱʱt��ֵ��t=0��![]() ��
��![]() ����3��S��t�ĺ�����ϵʽΪ��S=
����3��S��t�ĺ�����ϵʽΪ��S=![]() ����4��t��ֵΪ
����4��t��ֵΪ![]() ��
��![]() ��
��
����������������1�����ݹ��ɶ������AC�ij���Ȼ����AQ=AC-CQ��⼴�ɣ�
��2������P��AB�����˶�ʱ��PQ���ABC��һ�ߴ�ֱ���������������Q��C����P��A��ʱ��PQ��BC����PQ��ABʱ����PQ��ACʱ���ֱ���⼴����
��3����P��AB����ʱ����0��t��1����PG��AC��G����P�ڱ�BC��ʱ����1��t��3���ֱ���������ε���������Ľ���ʽ������
��4������APQ����PQΪ���ĵ���������ʱ��������������ٵ�P�ڱ�AB��ʱ����PG��AC��G����AG=GQ���з���������ڵ�P�ڱ�AC��ʱ�� AQ=PQ�����ݹ��ɶ������.
��⣺��1����ͼ1��
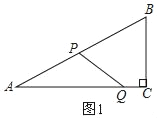
Rt��ABC�У���A=30�㣬AB=8��
��BC=![]() AB=4��
AB=4��
��AC=![]() ��
��
������ã�CQ=![]() t��
t��
��AQ=4![]() ��
��![]() t��
t��
��2������P��AB�����˶�ʱ��PQ���ABC��һ�ߴ�ֱ�������������
�ٵ�Q��C����P��A��ʱ��PQ��BC����ʱt=0��
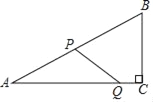
�ڵ�PQ��ABʱ����ͼ2��
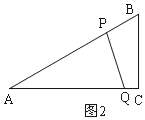
��AQ=4![]() ��
��![]() t��AP=8t����A=30�㣬
t��AP=8t����A=30�㣬
��cos30��=![]() ��
��
��![]() ��
��
t=![]() ��
��
�۵�PQ��ACʱ����ͼ3��
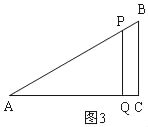
��AQ=4![]() ��
��![]() t��AP=8t����A=30�㣬
t��AP=8t����A=30�㣬
��cos30��=![]() ��
��
��![]()
t=![]() ��
��
��������������P��AB�����˶�ʱ��PQ���ABC��һ�ߴ�ֱʱt��ֵ��t=0��![]() ��
��![]() ��
��
��3�������������
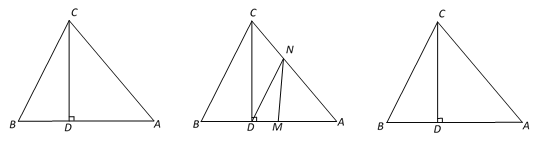
�ٵ�P��AB����ʱ����0��t��1����ͼ4����PG��AC��G��
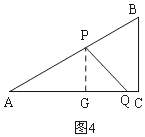
�ߡ�A=30�㣬AP=8t����AGP=90�㣬
��PG=4t��
��S��APQ=![]() AQPG=
AQPG=![]() ��4
��4![]() ��
��![]() t��4t=��2
t��4t=��2![]() t2+8
t2+8![]() t��
t��
�ڵ�P�ڱ�BC��ʱ����1��t��3����ͼ5��
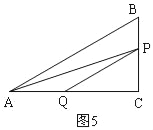
������ã�PB=2��t��1����
��PC=4��2��t��1��=��2t+6��
��S��APQ=![]() AQPC=
AQPC=![]() ��4
��4![]() ��
��![]() t������2t+6��=
t������2t+6��=![]() t2
t2![]() ��
��
����������S��t�ĺ�����ϵʽΪ��S=![]() ��
��
��4������APQ����PQΪ���ĵ���������ʱ�������������
�ٵ�P�ڱ�AB��ʱ����ͼ6��
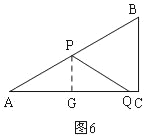
AP=PQ����PG��AC��G����AG=GQ��
�ߡ�A=30�㣬AP=8t����AGP=90�㣬
��PG=4t��
��AG=4![]() t��
t��
��AQ=2AG�ã�4![]() ��
��![]() t=8
t=8![]() t��t=
t��t=![]() ��
��
�ڵ�P�ڱ�AC��ʱ����ͼ7��AQ=PQ��
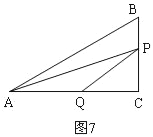
Rt��PCQ�У��ɹ��ɶ����ã�CQ2+CP2=PQ2��
��![]() ��
��
t=![]() ��
��![]() ���ᣩ��
���ᣩ��
����������t��ֵΪ![]() ��
��![]() ��
��

 Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�