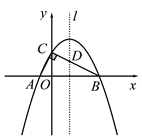题目内容
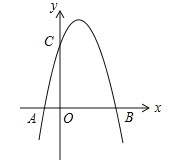
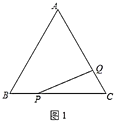
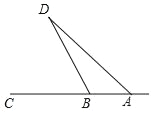
【题目】在等边![]() 中,点
中,点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 的延长线上,
的延长线上,![]() (如图1)
(如图1)
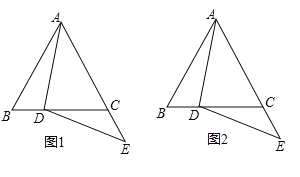
(1)求证:![]() ;
;
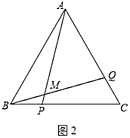
(2)点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() ,
,![]() .
.
①依题意将图2补全;
②证明:在点![]() 运动的过程中,始终有
运动的过程中,始终有![]() .
.
【答案】(1)证明见解析;(2)①补图见解析;②证明见解析.
【解析】
(1)先根据等腰三角形的性质可得![]() ,再根据等边三角形的性质可得
,再根据等边三角形的性质可得![]() ,然后根据角的和差、三角形的外角性质即可得证;
,然后根据角的和差、三角形的外角性质即可得证;
(2)①过点E作![]() ,交BC的延长线于点F,延长EF,使得
,交BC的延长线于点F,延长EF,使得![]() ,则点M即为点E关于BC的对称点,然后连接DM、AM即可;
,则点M即为点E关于BC的对称点,然后连接DM、AM即可;
②先根据轴对称的性质得出![]() ,再由题(1)可知
,再由题(1)可知![]() ,然后根据等边三角形的性质、角的和差可求出
,然后根据等边三角形的性质、角的和差可求出![]() ,从而可得
,从而可得![]() 是等边三角形,由等边三角形的性质即得证.
是等边三角形,由等边三角形的性质即得证.
(1)![]()
![]()
![]() 是等边三角形
是等边三角形
![]()
又![]()
![]() ;
;
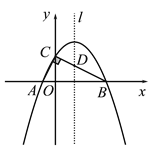
(2)①过点E作![]() ,交BC的延长线于点F,延长EF,使得
,交BC的延长线于点F,延长EF,使得![]() ,则点M即为点E关于BC的对称点,然后连接DM、AM,作图结果如下:
,则点M即为点E关于BC的对称点,然后连接DM、AM,作图结果如下:
②由轴对称得:![]()
![]()
![]()
由(1)可知:![]()
![]()
在![]() 中,
中,![]()
![]()
![]()
![]() 是等边三角形
是等边三角形
![]() .
.

练习册系列答案
相关题目