题目内容
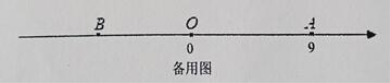
【题目】如图,已知数轴上点![]() 表示的数为9,
表示的数为9,![]() 是数轴上一点且
是数轴上一点且![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为
出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为![]() (
(![]() )秒.
)秒.
![]()
发现:
(1)写出数轴上点![]() 表示的数 ,点
表示的数 ,点![]() 表示的数 (用含
表示的数 (用含![]() 的代数式表示);
的代数式表示);
探究:
(2)动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿数轴向左匀速运动, 若点
出发,以每秒2个单位长度的速度沿数轴向左匀速运动, 若点![]() 、
、![]() 同时出发,问
同时出发,问![]() 为何值时点
为何值时点![]() 追上点
追上点![]() ?此时
?此时![]() 点表示的数是多少?
点表示的数是多少?
(3)若![]() 是线段
是线段![]() 靠近点
靠近点![]() 的三等分点,
的三等分点,![]() 是线段
是线段![]() 靠近点
靠近点![]() 的三等分点.点
的三等分点.点![]() 在运动的过程中, 线段
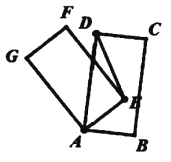
在运动的过程中, 线段![]() 的长度是否发生变化?在备用图中画出图形,并说明理由.
的长度是否发生变化?在备用图中画出图形,并说明理由.

拓展:
(4)若点![]() 是数轴上点,点
是数轴上点,点![]() 表示的数是
表示的数是![]() ,请直接写:
,请直接写:![]() 的最小值是 .
的最小值是 .
【答案】(1)-6;9-5t;(2)点P运动5秒时,在点C处追上点Q,P点表示的数是-16;(3)线段MN的长度不发生变化,其值为1;画出图形,理由见解析;(4)15.
【解析】
(1)设出B点表示的数为x,由数轴上两点间的距离即可得到x的方程,解方程即可得出x,由路程=速度×时间可得出点P走过的路程,再求得![]() 点表示的数;
点表示的数;
(2)设经t秒后P点追上Q点,根据题意可得,关于t的一元一次方程,解方程即可得出时间t;
(3)由P点位置的不同分两种情况考虑,依据三等分点的定义,可以找到线段间的关系,从而能找出MN的长度;
(4) 分![]() 及
及![]() 三种情况,解方程即可得出结论.
三种情况,解方程即可得出结论.
(1) 设B点表示![]() ,则有:
,则有:![]() ,解得:
,解得:![]() ,
,
∵动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,
∴经t秒后点P走过的路程为![]() ,
,
∴![]() 点表示的数为:
点表示的数为:![]() ,
,
故答案为![]() ;
;
(2)设点P运动t秒时,在点C处追上点Q(如图)
![]()
则AC=5t,BC=2t,
∵AC-BC=AB ,
∴5t-2t=15 ,
解得:t=5,
∴点P运动5秒时,在点C处追上点Q,
当![]() 时,
时,![]() ,
,
此时P点表示的数是![]() ;
;
(3)没有变化.
∵M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点,
∴![]() ,
,![]() .
.
分两种情况:

①当点P在点A、B两点之间运动时(如备用图):
所以MN=MP+NP=![]() AP+
AP+![]() BP=
BP=![]() (AP+BP)=
(AP+BP)=![]() AB=10
AB=10
②当点P运动到点B的左侧时(如备用图):

所以MN=MP-NP=![]() AP-
AP-![]() BP=
BP=![]() (AP-BP)=
(AP-BP)=![]() AB=10
AB=10
综上所述,线段MN的长度不发生变化,其值为10.
(4) ①当![]() 时,
时,![]() ,
,
∵![]()
∴![]() ,不存在最小值;
,不存在最小值;
②当![]() 时,
时,![]() ,
,
③当![]() 时,
时,![]() ,
,
∵![]()
∴![]() ,不存在最小值;
,不存在最小值;
综上,当![]() 时,
时,![]() 的最小值是
的最小值是![]() .
.
故答案为:15.

【题目】阅读下列材料:
材料一:
早在2011年9月25日,北京故宫博物院就开始尝试网络预售门票,2011年全年网络售票仅占1.68%.2012年至2014年,全年网络售票占比都在2%左右.2015年全年网络售票占17.33%,2016年全年网络售票占比增长至41.14%.2017年8月实现网络售票占比77%.2017年10月2日,首次实现全部网上售票.与此同时,网络购票也采用了“人性化”的服务方式,为没有线上支付能力的观众提供代客下单服务.实现全网络售票措施后,在北京故宫博物院的精细化管理下,观众可以更自主地安排自己的行程计划,获得更美好的文化空间和参观体验.
材料二:
以下是某同学根据网上搜集的数据制作的2013-2017年度中国国家博物馆参观人数及年增长率统计表.
年度 | 2013 | 2014 | 2015 | 2016 | 2017 |
参观人数(人次) | 7 450 000 | 7 630 000 | 7 290 000 | 7 550 000 | 8 060 000 |
年增长率(%) | 38.7 | 2.4 | -4.5 | 3.6 | 6.8 |

他还注意到了如下的一则新闻:2018年3月8日,中国国家博物馆官方微博发文,宣布取消纸质门票,观众持身份证预约即可参观. 国博正在建设智慧国家博物馆,同时馆方工作人员担心的是:“虽然有故宫免(纸质)票的经验在前,但对于国博来说这项工作仍有新的挑战.参观故宫需要观众网上付费购买门票,他遵守预约的程度是不一样的.但(国博)免费就有可能约了不来,挤占资源,所以难度其实不一样.” 尽管如此,国博仍将积极采取技术和服务升级,希望带给观众一个更完美的体验方式.
根据以上信息解决下列问题:
(1)补全以下两个统计图;
(2)请你预估2018年中国国家博物馆的参观人数,并说明你的预估理由.