Question

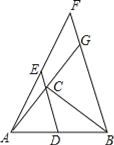
【题目】如图，△ABC中，∠C=90°，AC=3，BC=4，点D是AB的中点，点E在DC的延长线上，且CE=CD，过点B作BF∥DE交AE的延长线于点F，交AC的延长线于点G．

（1）求证：AB=BG；

（2）若点P是直线BG上的一点，试确定点P的位置，使△BCP与△BCD相似．

Answer 1

【答案】（1）证明见解析；（2）当PB=2.5或时，△BCP与△BCD相似．

【解析】试题分析：（1）利用平行分线段成比例定理得出，进而得出△ABC≌△GBC（SAS），即可得出答案；
（2）分别利用第一种情况：若∠CDB=∠CPB，第二种情况：若∠PCB=∠CDB，进而求出相似三角形即可得出答案．

试题解析：（1）证明：∵BF∥DE，

∴，

∵AD=BD，

∴AC=CG，AE=EF，

在△ABC和△GBC中：

，

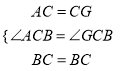∴△ABC≌△GBC（SAS），

∴AB=BG；

（2）当BP长为或时，△BCP与△BCD相似；

∵AC=3，BC=4，

∴AB=5，

∴CD=2.5，

∴∠DCB=∠DBC，

∵DE∥BF，

∴∠DCB=∠CBP，

∴∠DBC=∠CBP，

第一种情况：若∠CDB=∠CPB，如图1：

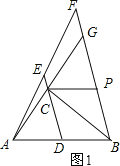
在△BCP与△BCD中

，

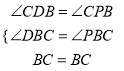∴△BCP≌△BCD（AAS），

∴BP=CD=2.5；

第二种情况：若∠PCB=∠CDB，过C点作CH⊥BG于H点．如图2：

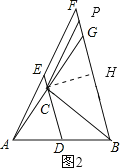
∵∠CBD=∠CBP，

∴△BPC∽△BCD，

∵CH⊥BG，

∴∠ACB=∠CHB=90°，∠ABC=∠CBH，

∴△ABC∽△CBH，

∴，

∴BH=，BP=．

综上所述：当PB=2.5或时，△BCP与△BCD相似．