Question

两个三角形中：
①两边及一角分别对应相等，
②两角及一边分别相等，
③三个角分别对应相等，
④三边分别对应相等，
⑤直角边、斜边分别对应相等．
不一定能保证两个三角形全等的命题的个数有

1. A.
   1个
2. B.
   2个
3. C.
   3个
4. D.
   4个

Answer 1

C
分析：全等三角形的判定定理有SAS，ASA，AAS，SSS，直角三角形的全等的判定定理还有HL，根据定理结合图形判断即可．
解答：∵全等三角形的判定定理有SAS，ASA，AAS，SSS，
∴两边及一角分别对应相等中，当这个角是其中一边的对角时，就不一定两三角形全等，错误，∴①正确；
两角及一边分别相等，如图：

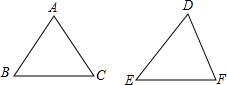
假如∠B=∠E，∠C=∠F，AB=DF时，两三角形就不全等，错误；∴②正确；
三个角分别对应相等，如图，

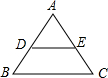
DE∥BC，△ADE和△ABC的三角对应相等，但两三角形不全等，错误；∴③正确；
三边分别对应相等，符合SSS，能推出两三角形全等，正确，∴④错误；
根据HL定理，有直角边、斜边分别对应相等的两直角三角形全等，正确，∴⑤错误；
故选C．
点评：本题考查了全等三角形的判定定理的应用，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS，直角三角形的全等的判定定理还有HL，题目比较典型，但是一道比较容易出错的题目．