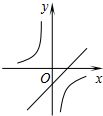题目内容
3.如果关于x的一元二次方程kx2-3x-1=0有两个不相等的实根,那么k的取值范围是k>-$\frac{9}{4}$且k≠0.分析 根据一元二次方程的定义和△的意义得到k≠0且△>0,即(-3)2-4×k×(-1)>0,然后解不等式即可得到k的取值范围.
解答 解:∵关于x的一元二次方程kx2-3x-1=0有两个不相等的实数根,
∴k≠0且△>0,即(-3)2-4×k×(-1)>0,
解得:k>-$\frac{9}{4}$且k≠0.
故答案为:k>-$\frac{9}{4}$且k≠0.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义.

练习册系列答案
相关题目
14.下列实数中,有理数是( )
| A. | $\sqrt{8}$ | B. | $\root{3}{4}$ | C. | $\frac{π}{2}$ | D. | 0.101001001 |
18.在实数-$\frac{1}{3}$,-2,0,$\sqrt{3}$中,最小的实数是( )
| A. | -2 | B. | 0 | C. | -$\frac{1}{3}$ | D. | $\sqrt{3}$ |
8.如图,是由若干个大小相同的正方体搭成的几何体的三视图,该几何体所用的正方体的个数是( )


| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
12.下列运算正确的是( )
| A. | x3+x2=x5 | B. | a3•a4=a12 | C. | (-x3)2÷x5=1 | D. | (-xy)3•(-xy)-2=-xy |
1.给出下列说法:①直径是弦;②弦是直径;③半圆是弧;④直径是圆中最长的弦.其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,△ABC的面积为6,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,P为直线AD上的一点,则线段BP的长不可能是( )
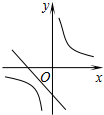
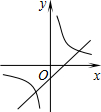
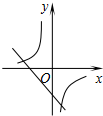
如图,△ABC的面积为6,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,P为直线AD上的一点,则线段BP的长不可能是( )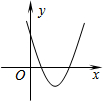 二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数$y=-\frac{a}{x}$与一次函数y=bx-c在同一坐标系内的图象大致是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数$y=-\frac{a}{x}$与一次函数y=bx-c在同一坐标系内的图象大致是( )