题目内容
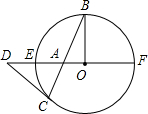 A是⊙O的直径EF上的一点,半径OB⊥EF,BA的延长线与⊙O相交于另一点C,若
A是⊙O的直径EF上的一点,半径OB⊥EF,BA的延长线与⊙O相交于另一点C,若 |
| EC |
| 1 |
| 5 |
 |
| CF |
(1)求∠B的度数;
(2)过C作⊙O的切线CD和OA的延长线交于点D.求证:AC=CD=AD.
分析:(1)本小题主要是通过弧与所对圆心角之间的关系来解决问题的
(2)此题主要是通过证明△ADC为等边三角形来解决问题.
(2)此题主要是通过证明△ADC为等边三角形来解决问题.
解答: (1)解:连接CO,
(1)解:连接CO,
∵
=
,
是半圆,
∴
=
=30°
∴∠EOC=3O°.
∵OB=OC,
∴∠B=∠BCO.
∴∠B=
(90°-∠EOC)
=
(90°-30°)
=30°.(4分)
(2)证明:∵∠DAC=∠BAO=90°-∠B=60°,
∠DCA=90°-∠OCA,
∠OBA=∠OCA=30°,
∴∠DAC=∠DCA=60°.
于是∠CDA=60°.(8分)
∴△ACD是等边三角形.
即AC=CD=AD.(10分)
 (1)解:连接CO,
(1)解:连接CO,∵
 |
| EC |
| 1 |
| 5 |
 |
| CF |
 |
| EF |
∴
 |
| EC |
| 1 |
| 6 |
 |
| EF |
∴∠EOC=3O°.
∵OB=OC,
∴∠B=∠BCO.
∴∠B=
| 1 |
| 2 |
=
| 1 |
| 2 |
=30°.(4分)
(2)证明:∵∠DAC=∠BAO=90°-∠B=60°,
∠DCA=90°-∠OCA,
∠OBA=∠OCA=30°,
∴∠DAC=∠DCA=60°.
于是∠CDA=60°.(8分)
∴△ACD是等边三角形.
即AC=CD=AD.(10分)
点评:本题主要是考查学生对圆的切线性质,圆心角和弧之间的关系,等边三角形的判定的掌握程度.解题的关键是发现圆心角和弧之间的关系,从而解决问题.

练习册系列答案
相关题目
 A是⊙O的直径EF上的一点,半径OB⊥EF,BA的延长线与⊙O相交于另一点C,若
A是⊙O的直径EF上的一点,半径OB⊥EF,BA的延长线与⊙O相交于另一点C,若 =
=
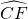 .
.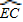 =
=
 .
.
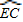 =
=
 .
.
 =
=
 .
.