题目内容
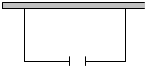 如图所示,要用防护网围成长方形花坛,其中一面利用现有的一段墙,且在与墙平行的一边开一个2米宽的门,现有防护网的长度为14米,花坛的面积需要24平方米,
如图所示,要用防护网围成长方形花坛,其中一面利用现有的一段墙,且在与墙平行的一边开一个2米宽的门,现有防护网的长度为14米,花坛的面积需要24平方米,(1)若墙的长度不限,求花坛的长和宽.
(2)若墙长8米,求花坛的长和宽.
分析:(1)设垂直于墙的一边长为x米,则平行于墙的一边长为(14-2x+2)米,根据矩形面积公式可列出方程,求出答案.
(2)利用(1)中所求,再利用墙长8米进而分析得出答案即可.
(2)利用(1)中所求,再利用墙长8米进而分析得出答案即可.
解答:解:(1)由题意得x•(14-2x+2)=24,
整理,得x2-8x+12=0,
解得x1=2,x2=6,
当垂直于墙的边长为2米,则平行于墙的长度为14-4+2=12(米),
当垂直于墙的边长为6米,则平行于墙的长度为14-12+2=4(米);
答:花坛的长和宽分别为12米,2米或花坛的长和宽分别为6米,4米.
(2)若墙长8米,当垂直于墙的边长为2米,则平行于墙的长度为14-4+2=12>8(不合题意舍去),
故垂直于墙的边长为6米,则平行于墙的长度为14-12+2=4(米).
答:花坛的长和宽分别为6米,4米.
整理,得x2-8x+12=0,
解得x1=2,x2=6,
当垂直于墙的边长为2米,则平行于墙的长度为14-4+2=12(米),
当垂直于墙的边长为6米,则平行于墙的长度为14-12+2=4(米);
答:花坛的长和宽分别为12米,2米或花坛的长和宽分别为6米,4米.
(2)若墙长8米,当垂直于墙的边长为2米,则平行于墙的长度为14-4+2=12>8(不合题意舍去),
故垂直于墙的边长为6米,则平行于墙的长度为14-12+2=4(米).
答:花坛的长和宽分别为6米,4米.
点评:本题主要考查一元二次方程的应用,解答本题的关键在于利用图形得出平行于墙的一边长为(14-2x+2)米.

练习册系列答案
相关题目
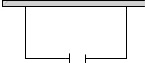
 如图所示,要用防护网围成长方形花坛,其中一面利用现有的一段墙,且在与墙平行的一边开一个2米宽的门,现有防护网的长度为14米,花坛的面积需要24平方米,
如图所示,要用防护网围成长方形花坛,其中一面利用现有的一段墙,且在与墙平行的一边开一个2米宽的门,现有防护网的长度为14米,花坛的面积需要24平方米,
