顶角为60°的等腰三角形.两个底角的平分线相交所成的角是120°．题目和参考答案——青夏教育精英家教网—

题目内容

18、顶角为60°的等腰三角形，两个底角的平分线相交所成的角是

120

°．

分析：等腰三角形的两底角相等，已知顶角大小，即可算出底角大小，然后根据三角形内角和为180°，即可算出两个底角的平分线相交所成的锐角．

解答：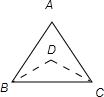

解：如图所示：
因为△ABC是等腰三角形且∠A=60°，所以∠ABC=∠ACB=60°，
又因为BD，CD分别平分∠ABC和∠ACB，
所以∠DBC=∠DCB=30°，所以∠BDC=120°，
所以两个底角的平分线相交所成的角是120°
故填120．

点评：本题主要考查对于等腰三角形的性质及三角形内角和定理；做题时要注意题中要问的问题是“两个底角的平分线相交所成的锐角”，容易答成120°钝角．

练习册系列答案

基础章节总复习测试卷系列答案

2点备考案系列答案

68所名校图书全国著名重点中学3年招生试卷及预测试题精选系列答案

（填“是”或“不是”）．
（2）小丽经过三次折叠发现了∠BAC是△ABC的好角，请探究∠B与∠C（不妨设∠B＞∠C）之间的等量关系．根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为

∠B=n∠C

．
应用提升
（3）小丽找到一个三角形，三个角分别为15°、60°、105°，发现60°和105°的两个角都是此三角形的好角．
请你完成，如果一个三角形的最小角是4°，试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．

阅读理解
如图1，△ABC中，沿∠BAC的平分线AB₁折叠，剪掉重叠部分；将余下部分沿∠B₁A₁C的平分线A₁B₂折叠，剪掉重叠部分；将余下部分沿∠B_nA_nC的平分线A_nB_n+1折叠，点B_n与点C重合．无论折叠多少次，只要最后一次恰好重合，我们就称∠BAC是△ABC的好角．

小丽展示了确定∠BAC是△ABC的好角的两种情形．
情形一：如图2，沿等腰三角形ABC顶角∠BAC的平分线AB₁折叠，点B与点C重合；

情形二：如图3，沿 △ABC的∠BAC的平分线AB₁折叠，剪掉重叠部分；
将余下的部分沿∠B₁A₁C的平分线 A₁B₂折叠，此时点B₁与点C重合．

探究发现
（1）△ABC中，∠B=2∠C，经过两次折叠，∠BAC （填“是”或“不是”）△ABC的好角；
（2）若经过三次折叠发现∠BAC是△ABC的好角，请探究∠B与∠C之间的等量关系（不妨设∠B>∠C）．
根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C之问的等量关系为．（不妨设∠B>∠C）
应用提升：
（3）小丽找到一个三角形，三个角分别为15º，60º，l05º，发现60º和l05º的两个角都是此三角形的好角．
请你完成，如果一个三角形的最小角是4º，试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．