题目内容
18、如图,AD是直角三角形ABC斜边上的中线,AE⊥AD交CB延长线于E,则图中一定相似的三角形是( )

分析:根据等腰三角形底角相等的性质可得∠C=∠DAC,易证∠BAE=∠DAC,即可证明∠C=∠BAE,∴即可证明△AEB与△ACD.
解答:证明:∵斜边中线长为斜边的一半,
∴AD=BC=CD,
∴∠C=∠DAC,
∵∠BAE+∠BAD=90°,∠DAC+∠BAD=90°,
∴∠BAE=∠DAC,
∴∠C=∠BAE,
∵∠E=∠E,
∴△BAE∽△ACE( ),
故选 C.
∴AD=BC=CD,
∴∠C=∠DAC,
∵∠BAE+∠BAD=90°,∠DAC+∠BAD=90°,
∴∠BAE=∠DAC,
∴∠C=∠BAE,
∵∠E=∠E,
∴△BAE∽△ACE( ),
故选 C.
点评:本题考查了相似三角形的证明,考查了等腰三角形底角相等的性质,本题中求证∠C=∠BAE是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
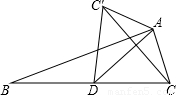
 12、如图,AD是直角三角形△ABC斜边上的中线,把ADC沿AD对折,点C落在点C′处,连接CC′,则图中共有等腰三角形
12、如图,AD是直角三角形△ABC斜边上的中线,把ADC沿AD对折,点C落在点C′处,连接CC′,则图中共有等腰三角形