题目内容
如图，在⊙O中，直径AB丄弦CD于点M，AM=18，BM=8，则CD的长为 ．
【答案】分析：连接OD，由AM=18，BM=8可求出⊙O的半径，利用勾股定理可求出MD的长，再根据垂径定理即可得出CD的长．
解答：
解：连接OD，
∵AM=18，BM=8，
∴OD=
=
=13，
∴OM=13-8=5，
在Rt△ODM中，DM=
=
=12，
∵直径AB丄弦CD，
∴CD=2DM=2×12=24．
故答案为：24．
点评：本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
解答：
解：连接OD，∵AM=18，BM=8，
∴OD=
==13，∴OM=13-8=5，
在Rt△ODM中，DM=
==12，∵直径AB丄弦CD，
∴CD=2DM=2×12=24．
故答案为：24．
点评：本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
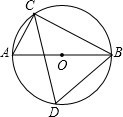如图，在⊙O中，直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，则BC=
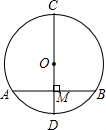如图，在⊙O中，直径CD的长度为10cm，AB是弦，且AB⊥CD于M，OM=3cm，求弦AB的长．
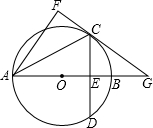C与直线AB相交于点G．
（2013•百色）如图，在⊙O中，直径CD垂直于弦AB，若∠C=25°，则∠ABO的度数是（ ）
（2012•朝阳区二模）如图，在⊙O中，直径AB⊥弦CD于点H，E是⊙O上的点，若∠BEC=25°，则∠BAD的度数为（ ）