Question

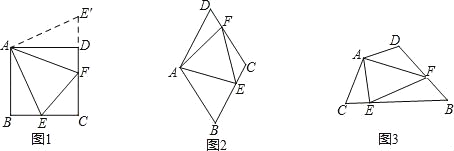
【题目】如图①，在△ABC中，AC=BC，点D为BC的中点，DE⊥AB，垂足为点E，过点B作BG∥AC交DE的延长线于点G.

（1）求证：DB=BG；

（2）当∠ACB=90°时，如图②，连接AD、CG，求证：AD⊥CG。

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】试题分析：（1）利用平行线的性质，和三角形全等得出结论；（2）利用三角形全等和等角的余角相等，解决问题.

试题解析：证明：（1）∵AC=BC ∴ ∠A=∠CBA

∵ AC∥BG ∴ ∠A=∠GBA即∠CBA=∠GBA

∵ DE⊥AB ∴ ∠DEB=∠GEB　

在△DBE和△GBE中

∴ △DBE≌△GBE

∴DB=BG

(2) ∵ 点D为BC的中点 ∴ CD=DB

∵ DB=BG ∴ CD=BG

∵ AC∥BG ∴ ∠ACB+∠GBC=180°

∵ ∠ACB=90° ∴∠GBC=∠ACB=90°

在△ACD和△CBG中

∴ △ACD≌△CBG

即∠CAD=∠BCG

∵ ∠ACG+∠BCG=90°

∴ ∠ACG+∠CAD=90°即 AD⊥CG