题目内容
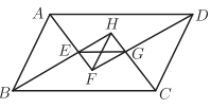
【题目】(本题满分12分)如图,Rt△![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为斜边
为斜边![]() 的中点,点
的中点,点![]() 为边
为边![]() 上的一个动点.连结
上的一个动点.连结![]() ,过点
,过点![]() 作
作![]() 的垂线与边
的垂线与边![]() 交于点
交于点![]() ,以
,以![]() 为邻边作矩形
为邻边作矩形![]() .
.
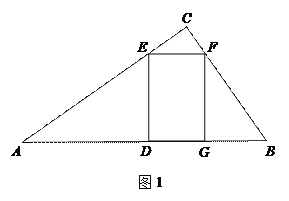
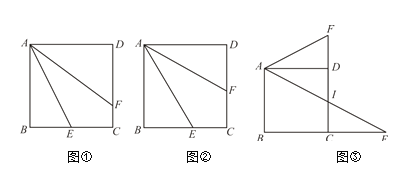
(1)如图1,当![]() ,点
,点![]() 在边
在边![]() 上时,求DE和EF的长;
上时,求DE和EF的长;
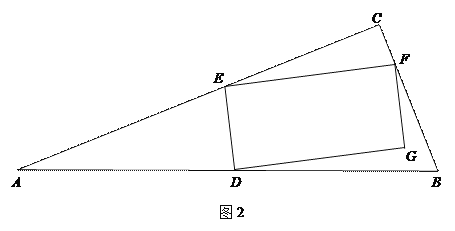
(2)如图2,若![]() ,设
,设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() ,求y关于
,求y关于![]() 的函数表达式;
的函数表达式;
(3)若![]() ,且点
,且点![]() 恰好落在Rt△
恰好落在Rt△![]() 的边上,求
的边上,求![]() 的长.
的长.
【答案】(1)![]() ;
; ![]() ;(2)
;(2)![]() ;(3)9或12.
;(3)9或12.
【解析】试题分析:(1)根据勾股定理求出AB,根据相似三角形的判定定理得到△ADE∽△ACB,根据相似三角形的性质求出DE和BG,求出EF;
(2)作DH⊥AC于H,根据相似三角形的性质得到y关于x的函数解析式;
(3)根据点G在边BC上和点G在边AB上两种情况,根据相似三角形的性质解答.
解:(1)∵∠ACB=90°,BC=6,AC=8,
∴AB= =10,
∵D为斜边AB的中点,
∴AD=BD=5,
∵DEFG为矩形,
∴∠ADE=90°,
∴∠ADE=∠C,又∠A=∠A,
∴△ADE∽△ACB,
∴AD:AC=DE:BC,即5:8=DE:6,
解得,DE=![]() ,
,
∵△ADE∽△FGB,
∴AD:GF=DE:BG,
则BG=![]() ,
,
∴EF=DG=AB-AD-BG=![]() ;
;
(2)过点![]() 作
作![]() 于点
于点![]() , 从而
, 从而![]() .
.
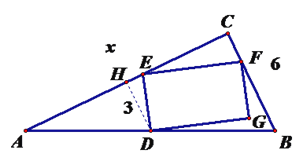
易得△![]() ∽△
∽△![]() ,
,
由![]() , 可得
, 可得![]() ,
, ![]() .
.
所以![]() .
.
∴![]() .
.
(3)由题意,点![]() 可以在边
可以在边![]() 或者
或者![]() 上.
上.
①若点![]() 在边
在边![]() 上,
上,
由![]() ,可知
,可知![]() ,于是
,于是![]() ;
;
②若点![]() 在边
在边![]() 上.
上.
记![]() ,矩形边长
,矩形边长![]() ,
,
由△![]() ∽△
∽△![]() , 可得
, 可得![]() , 即
, 即![]() ,
,
化简可得![]() , 因式分解后有:
, 因式分解后有: ![]() , 即
, 即![]() .
.
而由△![]() ∽△
∽△![]() , 所以
, 所以![]() , 从而
, 从而![]() .
.
综上知,AC的值为9或12.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目