题目内容
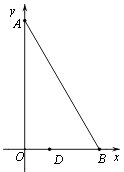
【题目】如图1，在四边形ABCD中，点E为AB延长线上一点，连接
并延长交AD延长线于点
，
，
.（1）求证：
；
图1
（2）如图2，连接
交
于点
，连接
，若为
的角平分线，
为
的角平分线，过点
作
交于点
， 求证：
；
图2
备用图
（3）在（2）的条件下，若
，
，求
的度数.
【答案】（1）见解析，（2）见解析，（3）
【解析】
（1）先根据平行线的判定证明AF∥BC，可得∠FDC=∠DCB，由已知可得∠CBE=∠DCB，由平行线的判定可得结论；
（2）先根据垂直得∠HBC=90°=∠CBE+∠ABH，设
，则∠ABH
，由平行线和角平分线的定义可推出
，
；
，即可得结论；
（3）根据第（2）的结论
，可得
，由三角形的内角和得
，根据已知
可得
，过点
作
，由平行线的性质及已知条件可得∠BFE=30°．
解：（1）
，
，
，
，
，
；
（2）过点
作
为
的角平分线，
为
的角平分线
，
设
由（1）问可知，
，
，
，
，
，
，
，
，
，
，
，
；
（3）由（2）得，
，
，
，
，
，
，
，
，
，
，
，
，
，
过点作
，
故答案为：（1）见解析，（2）见解析，（3） .
练习册系列答案
相关题目
