Question

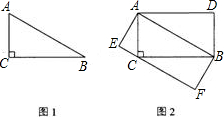
阅读下面短文：如图1，△ABC是直角三角形，∠C=90°，现将△ABC补成长方形，使△ABC的两个顶点为长方形一边的两个端点，第三个顶点落在长方形这一边的对边上，那么符合要求的长方形可以画出两个：长方形ACBD和长方形AEFB（如图2）。

解答问题：

（1）设图2中长方形ACBD和长方形AEFB的面积分别为S₁，S₂，则S₁    S₂（填“＞”、“＝”或“＜”）

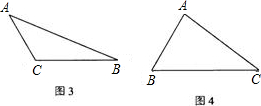
（2）如图3，△ABC是钝角三角形，按短文中的要求把它补成长方形，那么符合要求的长方形可以画出        个，利用图3把它画出来。

（3）如图4，△ABC是锐角三角形且三边满足BC＞AC＞AB，按短文中的要求把它补成长方形，那么符合要求的长方形可以画出       个，利用图4把它画出来。

（4）在（3）中所画出的长方形中，哪一个的周长最小？为什么？

 

Answer 1

【答案】

（1）=；（2）1；（3）3；（4）以AB为边的长方形。

【解析】

试题分析：（1）易得原有三角形都等于所画矩形的一半，那么这两个矩形的面积相等．

（2）可仿照图2矩形ABFE的画法得到矩形．由于∠C非直角，所以只有一种情况．

（3）可让原锐角三角形的任意一边为矩形的一边，另一顶点在矩形的另一边的对边上，可得三种情况．

（4）根据三个矩形的面积相等，利用求差法比较三个矩形的周长即可．

（1）=；

（2）1；

（3）3；

（4）以AB为边长的长方形周长最小，

设长方形BCED，ACHQ，ABGF的周长分别为，，，BC=a，AC=b，AB=c．易得三个长方形的面积相等，设为S，

，

，同理可得

∴以AB为边长的长方形周长最小．

考点：本题考查的是直角三角形的综合应用

点评：解决此题的关键是注意运用类比的方法画图；要比较两个数或式子的大小，一般采用求差法．