题目内容
 如图,矩形ABCD中,AC与BD的交点为E,若AB=6,BC=8,则DE=________.
如图,矩形ABCD中,AC与BD的交点为E,若AB=6,BC=8,则DE=________.
5
分析:由四边形ABCD为矩形,根据矩形的性质得到角ABC为直角,且对角线互相平分且相等,得到DE等于AC的一半,在直角三角形ABC中,由AB和BC的值,利用勾股定理即可求出AC的长度,进而得到DE的值.
解答:∵四边形ABCD为矩形,
∴∠ABC=90°,AE=CE=BE=DE= AC,
AC,
∴在直角三角形ABC中,根据勾股定理得:
AC2=AB2+BC2,又AB=6,BC=8,
∴AC= =10,
=10,
∴DE= AC=5.
AC=5.
故答案为:5.
点评:此题要求学生掌握矩形的性质,灵活运用勾股定理化简求值,是一道中档题.解本题的关键是学生要掌握矩形对角线的交点到矩形四个顶点的距离相等这个性质.
分析:由四边形ABCD为矩形,根据矩形的性质得到角ABC为直角,且对角线互相平分且相等,得到DE等于AC的一半,在直角三角形ABC中,由AB和BC的值,利用勾股定理即可求出AC的长度,进而得到DE的值.
解答:∵四边形ABCD为矩形,
∴∠ABC=90°,AE=CE=BE=DE=
 AC,
AC,∴在直角三角形ABC中,根据勾股定理得:
AC2=AB2+BC2,又AB=6,BC=8,
∴AC=
 =10,
=10,∴DE=
 AC=5.
AC=5.故答案为:5.
点评:此题要求学生掌握矩形的性质,灵活运用勾股定理化简求值,是一道中档题.解本题的关键是学生要掌握矩形对角线的交点到矩形四个顶点的距离相等这个性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
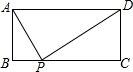 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )A、a≥
| ||
| B、a≥b | ||
C、a≥
| ||
| D、a≥2b |
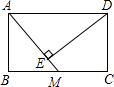 如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为
如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为 7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE=
7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE= (2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为
(2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为 (2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.
(2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.